本文提出了 Training Quantization Thresholds (TQT)：一种基于 QAT 的学习均匀、对称、Per-tensor 量化器的截断阈值的方法。TQT 在训练时使用了 STE ，并将量化步长限制在了 Power-of-Two，采用 PoT 形式的量化步长在推理时仅使用整型加法和移位运算，利于硬件部署。本文对 TQT 的鲁棒性进行了数学分析，并在多个 CNN 上进行了 ImageNet 图像分类任务。实验结果表明：TQT 在 MobileNet 等之前较难量化的神经网络上在少于 5 epochs 的训练就达到了接近浮点的精度。本文相关 Github 项目：Graffitist
- Title: Trained Quantization Thresholds for Accurate and Efficient Fix-point Inference of Deep Neural Networks
- Venue: MLSys 2020
- Author(s): Sambhav R. Jain, Albert Gural, Michael Wu, Chris H. Dick
- Institution(s): Xilinx Inc, Stanford University
- Link(s): arxiv:1903.08066
- Project(s): Graffitist, Vitis-AI
Introduction
本文主要关注以下三个问题：
- 之前的量化工作大部分是基于 PTQ 的静态量化，即对预训练模型进行校准得到的截断阈值在之后保持固定不变，相比 QAT 方法得到的量化截断阈值的泛化能力更差。
- PTQ 校准中定义的 Per-Tensor 或 Per-Channel 的 Quantization Error 所用的 Metrics (KLD、MSE等) 都是基于经验设计的。这些 Metrics 与模型最终的 Loss 是否存在相关性，现在业界依然没有理论上的数学证明。相比起那些优化人工给定的 Metrics 的 PTQ 方法，使用 Training-based 的方法更有效，在理论上也更有说服力。
- 2018 年 Google 的论文提出的 Integer-Only Inference 量化方案中的比例系数 M 是 dyadic 型的参数而非 PoT 型的参数，会存在一定的高位整型数存储和乘法运算，这会对硬件的存储和运算造成负担。更理想的全整型推理量化方案将量化步长限制在 PoT 的形式，这样可以完全用移位来代替量化步长的乘法运算，更利于硬件加速和实现。
Related Works
- STE arxiv:1308.3432
- Integer-Arithmetic-Only Inference (CVPR 2018) arxiv:1712.05877
- PACT arxiv:1805.06085
- LSQ (ICLR 2020) arxiv:1902.08153
Trained Quantization Thresholds (TQT)
Quantizer Constraints
TQT 的采用的均匀量化公式如下：
$$
r=s·(q-z)
\tag{2}
$$
其中 $s$ 为量化步长，$z$ 为量化零点，$q$ 为量化后的整型数值。为了简化量化运算，TQT采用了对称量化，令 $z=0$ 省略多项式乘法中含量化零点的展开项：
$$
r=s·q
\tag{3}
$$
同时，TQT 要求量化步长 $s$ 限制为 PoT 的形式，即 $s=2^{-f}$，其中 $f$ 为fractional length，可以理解为浮点数小数点的位置，是一个有符号整型数。这样在计算 $r=s·q$ 时就可以用移位运算代替乘法运算。
Forward Pass
TQT 完整的量化前向计算包含缩放 (Scaling)、取整 (Rounding)、截断 (Saturation)、反量化 (De-quant) 四个计算步骤，量化函数如下：
$$
q(x;s)=\text{clip} \left( \left\lfloor \frac{x}{s} \right\rceil ;n,p \right)·s
\tag{4}
$$
其中 $q(x;s)$ 表示量化函数，$x$ 表示输入 Tensor，$s$ 表示量化步长，$\text{clip}$ 表示区间限定函数，$n$ 和 $p$ 分别为区间上下界。
量化参数取值根据输入 Tensor 是否有符号决定。
- 输入为有符号数 (signed)：
$$
n=-2^{b-1}, p=2^{b-1}-1, s=\frac{2^{\left\lceil \text{log}_2\thinspace t \right\rceil}}{2^{b-1}}
$$ - 输入为无符号数 (unsigned)：
$$
n=0, p=2^b-1, s=\frac{2^{\left\lceil \text{log}_2\thinspace t \right\rceil}}{2^b}
$$
其中 $t$ 是原始的量化截断阈值，实际上的量化截断阈值的取值是大于 $t$ 的最小的 PoT 型数值 $2^{\left\lceil \text{log}_2\thinspace t \right\rceil}$。
Backward Pass
TQT 在训练过程中同时优化输入 $x$ 和量化步长 $s$。为了更方便表示反向传播的梯度，可以改写前向传播的量化函数中的 $\text{clip}$ 函数成为如下的分段函数形式：
$$
q(x;s)=
\left\lbrace
\begin{aligned}
& \left\lfloor \frac{x}{s} \right\rceil ·s && \text{if } n\leq\left\lfloor \frac{x}{s} \right\rceil \leq p, \\
& n·s && \text{if } \left\lfloor \frac{x}{s} \right\rceil < n, \\
& p·s && \text{if } \left\lfloor \frac{x}{s} \right\rceil > p. \\
\end{aligned}
\right.
\tag{5}
$$
在进行反向传播时，TQT 对不可反向传播的取整运算采用了 STE，即对于 $\left\lceil x \right\rceil \neq x, \left\lfloor x \right\rfloor \neq x, \left\lfloor x \right\rceil \neq x$ 的情况时，令$\frac{\partial \left\lceil x \right\rceil}{\partial x} = \frac{\partial \left\lfloor x \right\rfloor}{\partial x} = \frac{\partial \left\lfloor x \right\rceil}{\partial x} = 1$。
这样得到的量化函数 $q$ 关于 $x$ 和 $s$ 的梯度如下：
$$
\nabla_s q(x;s)=
\left\lbrace
\begin{aligned}
& \left\lfloor \frac{x}{s} \right\rceil - \frac{x}{s} && \text{if } n\leq\left\lfloor \frac{x}{s} \right\rceil \leq p, \\
& n && \text{if } \left\lfloor \frac{x}{s} \right\rceil < n, \\
& p && \text{if } \left\lfloor \frac{x}{s} \right\rceil > p. \\
\end{aligned}
\right.
\tag{6}
$$
注意到 $\nabla_{\text{log}_2 \thinspace t} s=s \text{ ln}(2)$，上式可继续转化为：
$$
\nabla _{\text{log}_2\thinspace t} q(x;s)=s \text{ ln}(2)·
\left\lbrace
\begin{aligned}
& \left\lfloor \frac{x}{s} \right\rceil - \frac{x}{s} && \text{if } n\leq\left\lfloor \frac{x}{s} \right\rceil \leq p, \\
& n && \text{if } \left\lfloor \frac{x}{s} \right\rceil < n, \\
& p && \text{if } \left\lfloor \frac{x}{s} \right\rceil > p. \\
\end{aligned}
\right.
\tag{7}
$$
同理，输入 $x$ 的梯度如下：
$$
\nabla _x q(x;s)=
\left\lbrace
\begin{aligned}
& 1 && \text{if } n \leq \left\lfloor \frac{x}{s} \right\rceil \leq p, \\
& 0 && \text{otherwise} \\
\end{aligned}
\right.
\tag{8}
$$
Interpretation of Gradients
上面给出了量化器 $q$ 对 $x$ 和 $\text{log}_2 \thinspace t$ 的梯度公式，为了直观地理解量化器在 QAT 反向传播时梯度的变化情况，不妨考虑下面这样一个简单的场景：
使用最小平方误差 (least-square error) L2损失函数 $L = (q(x;s) - x)^2/2$ 优化一个 TQT 量化器，$L$ 对 $x$ 和 $\text{log}_2 \thinspace t$ 的梯度如下：
$$
\begin{align}
\nabla _{\text{log}_2 \thinspace t} L &= (q(x;s) - x) · \nabla _{\text{log}_2 \thinspace t} q(x;s) \tag{9}\\
\nabla _x L &= (q(x;s) - x) · (\nabla _x q(x;s) - 1) \tag{10}\\
\end{align}
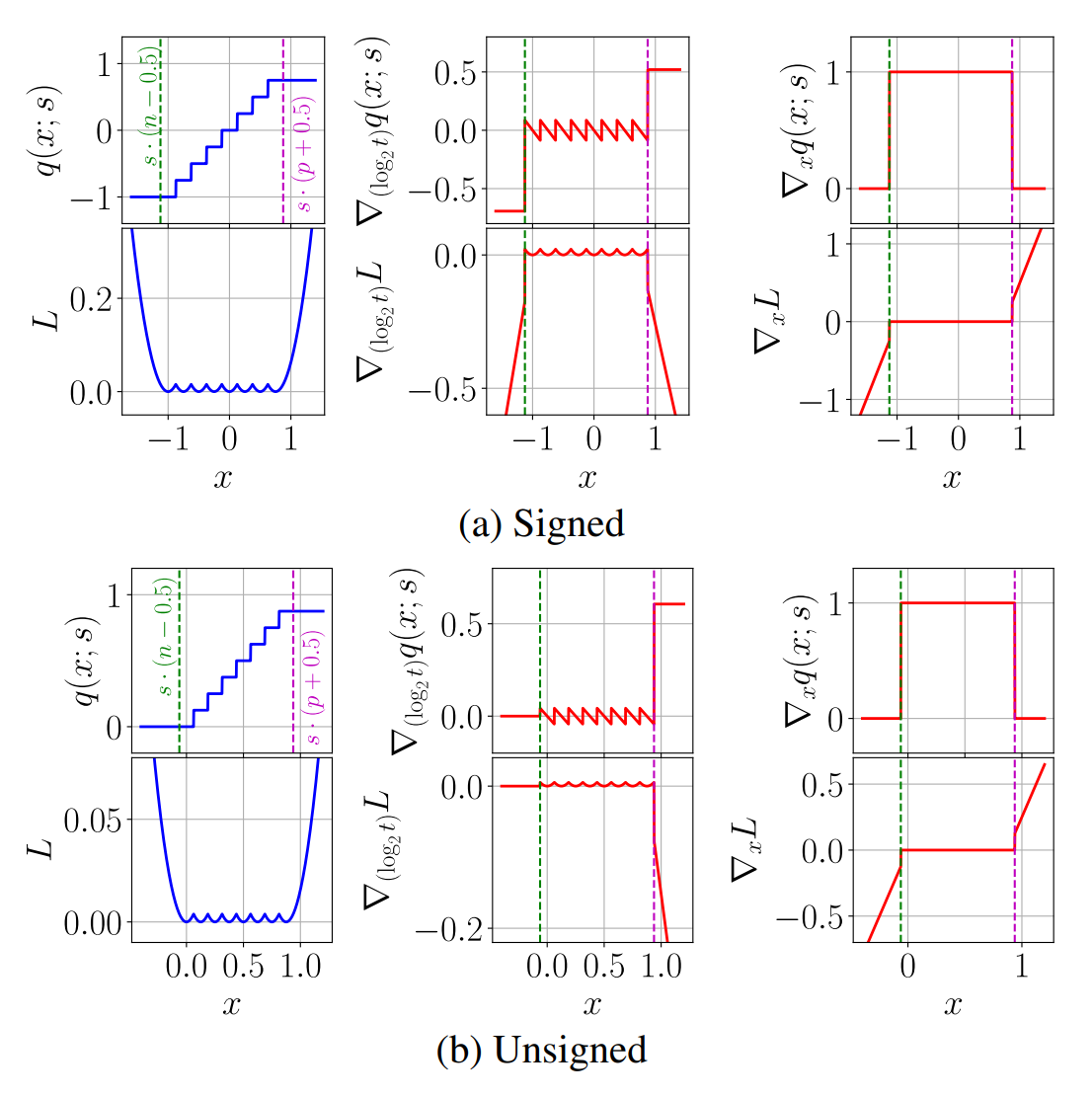$$
Figure 1
Figure 1 展示了在 $b=3, t=1.0$ 时有符号和无符号情况下函数值和各参数梯度的变化曲线。第一行为量化函数，第二行为损失函数。
考虑到取整 $\left\lfloor · \right\rceil$ 函数和截断 $\text{clip}$ 函数的共同作用，实际上输入 $x$ 的真实范围为 $[s·(n-0.5), s·(p+0.5)]$。从Figure 1可以看出：
- 当输入 $x$ 在真实范围内时，$L$ 对 $\text{log}_2 \thinspace t$ 的梯度非负，对 $x$ 的梯度为 $0$；
- 当输入 $x$ 在真实范围外时，$L$ 对 $\text{log}_2 \thinspace t$ 的梯度恒负，对 $x$ 的梯度左负右正。
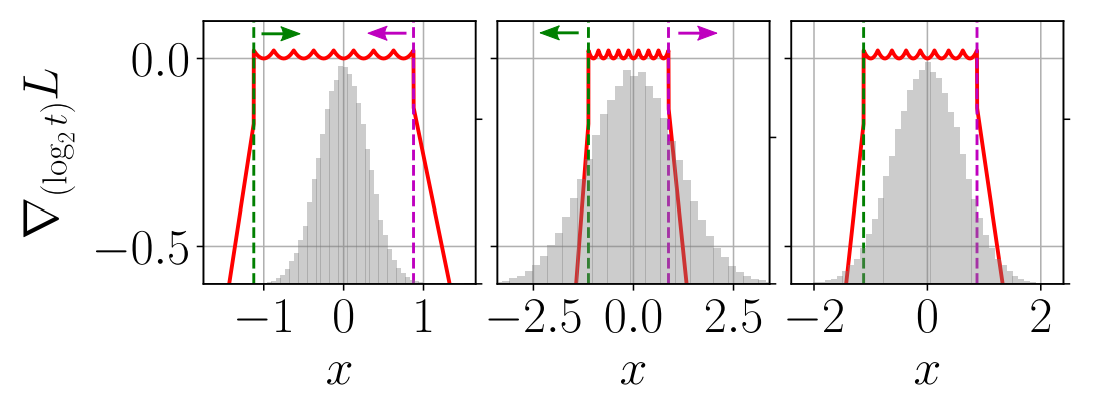Figure 2
Figure 2 展示了通常情况下呈钟型分布(例如高斯分布)的输入 $x$ 的 $\text{log}_2 \thinspace t$ 梯度的变化情况：
- 左图：绝大部分输入值 $x$ 都在真实范围内，对 $\text{log}_2 \thinspace t$ 的累计梯度为正，梯度下降更新使得 $\text{log}_2 \thinspace t$ 减小向分布中心靠近；
- 中间图：对于在真实范围外的输入，其对 $\text{log}_2 \thinspace t$ 的累计梯度为负，梯度下降使 $\text{log}_2 \thinspace t$ 向外扩大。
- 右图：训练收敛时，正负梯度相加为零，此时的截断阈值满足 PoT 型且能够使模型精度损失尽可能低。
TQT 在 QAT 过程中同时优化输入 $x$。与对截断阈值梯度的分析类似：
- 当输入 $x$ 在真实范围内时，$L$ 对 $x$ 的梯度为 $0$，即截断范围内输入保持不变；
- 当输入 $x$ 在真实范围外时，$L$ 对 $x$ 的梯度左负右正。
这表明，对于范围外的输入 $x$，梯度下降更新使得输入 $x$ 向范围内变化，使 $x$ 越来越趋向分布中心，减少分布中的离群点。
Comparison to Clipped Threshold Gradients
- 与 TensorFlow 的 FakeQuant 的比较
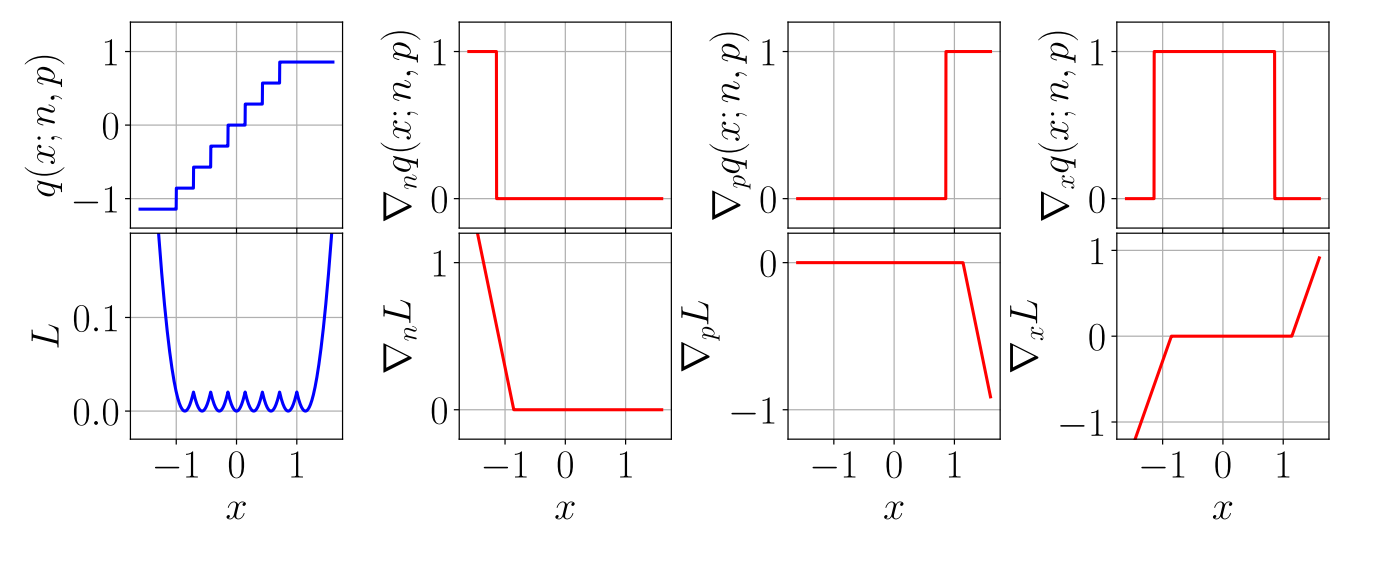Figure 3
TensorFlow 框架的伪量化模块 FakeQuant 参考的量化函数如下：
$$
q(x;n,p)=\left\lfloor \frac{\text{clip}(x;n,p)-n}{\frac{p-n}{2^b-1}} \right\rceil · \frac{p-n}{2^b-1} + n
\tag{11}
$$
Figure 3 展示了在 $b=3, n=-1.125, p=0.875$ 时 TensorFlow 的 FakeQuant 模块的函数值和各参数梯度的变化曲线。与TQT的量化方法相比，FakeQuant学习截断阈值 $n$ 和 $p$，在反向传播阶段将取整函数简化为恒等函数。由Figure 3可以看出， $n$ 和 $p$ 的梯度恒为正，因此在梯度下降更新时只能向外侧变化，这样的学习方法得到的结果更贴近于PTQ的min/max截断阈值取值，而不是在量化模型精度和截断范围之间进行trade-off。
- 与 PACT 的比较
PACT (PArameterized Clipping acTivation) 为了能够将量化截断阈值引入 QAT 训练过程中进行优化，提出了 Clipped ReLU 激活函数：
$$
y=PACT(x)=0.5(|x|-|x-\alpha|+\alpha)=
\left\lbrace
\begin{aligned}
& 0, && x \in (-\infty, 0) \\
& x, && x \in [0, \alpha) \\
& \alpha, && x \in [\alpha, +\infty) \\
\end{aligned}
\right.
$$
输出激活值对截断阈值 $\alpha$ 的梯度使用 STE 近似如下：
$$
\frac{\partial y_q}{\partial \alpha} =
\left\lbrace
\begin{aligned}
& 0, && x \in (-\infty, \alpha) \\
& 1, && x \in [\alpha, +\infty) \\
\end{aligned}
\right.
\tag{1}
$$
在 PACT 方法中，$\alpha$ 的梯度只与 $x$ 取值在 $\alpha$ 的哪一侧有关，显然只有在 $\alpha$ 右侧的值能够造成影响，因此在训练过程中 $\alpha$ 会趋向于 $x$ 的右端取值的最大值。为了避免这一现象，PACT 在训练时在损失函数中加入了对 $\alpha$ 的 L2 正则项，但是 L2 正则项的超参数 $\lambda_{\alpha}$ 只能人工设定，不能自动地在 QAT 过程中进行优化，因此相比 TQT 而言略显不足。有关 PACT 的其它具体细节请查阅相关文献和阅读笔记。
Framework of TQT
本文相关的 Github 项目 Graffitist 是基于 TensorFlow 框架和 TQT 方法实现的端到端式的量化解决方案。Graffitist 支持对多种神经网络进行计算图优化和模型量化。
Graph Optimizations
Graffitist 实现了多种对计算图的优化方式。包括 Fuse-BN、多重 concat 拆分成单一 concat、将平均池化层转化为深度卷积层等等。
Quantization Modes
Graffitist 实现了多种量化模式，包括 PTQ 的静态量化模式和 QAT 的量化模式。
Layer Precisions
Graffitist 分别实现了针对计算层、激活层、平均池化层和 concat 操作的量化计算位数设计。
Fused Kernel Implementation
Graffitist 中打包了为 CPU/GPU 预编译的融合后的量化内核。经过融合后的量化器占用内存低，从而可以使用更大的 batch size 来实现加速。
Experiments
此处只展示实验结果。省略了实验的初始化和实现细节，具体细节请参看原论文。
Results
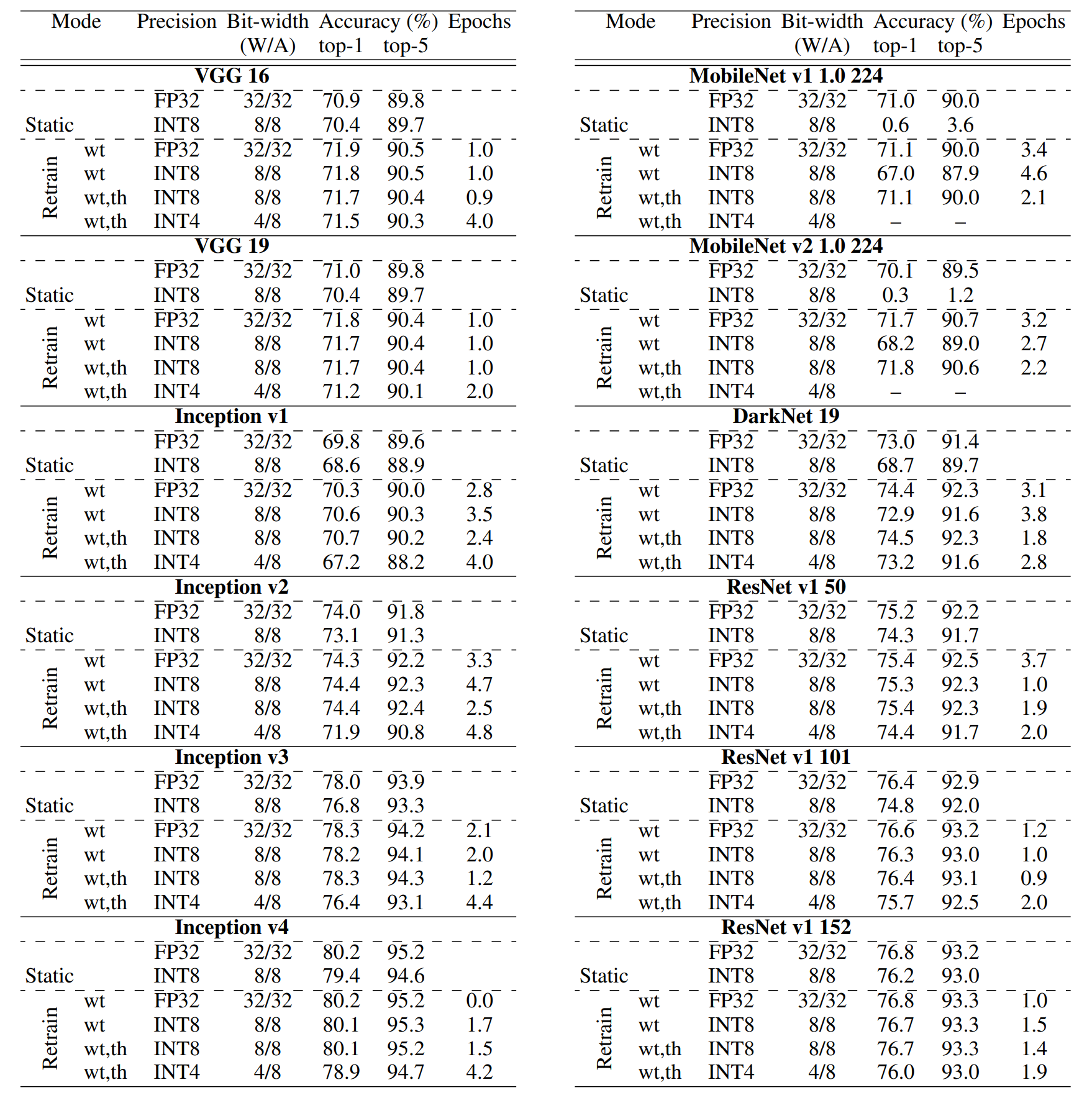Table 3
Discussion
Insights from TQT
本文观察到了关于 TQT 的一些值得注意的实验现象：
- QAT 方法得到的模型预测精度比 PTQ 静态量化的更高，这也是期望之中的结果。
- 对于 VGG、Inception、ResNet 等 INT8 量化难度较低的模型，固定截断阈值只对模型参数进行再训练的效果已经足够好了，此时也采用 TQT 方法也没有更多精度上的提升。
- 对于 MobileNet、DarkNet 等 INT8 量化难度较高的模型，同时训练模型参数与截断阈值要比只训练模型参数的精度高 $4 \%$，甚至接近 FP32 模型的精度。
- 对于更低比特的 INT4 量化，只训练模型参数已经很难提升精度了，因此 INT4 量化必须使用 TQT 方法才能有效维持模型精度。
MobileNet Comparisons
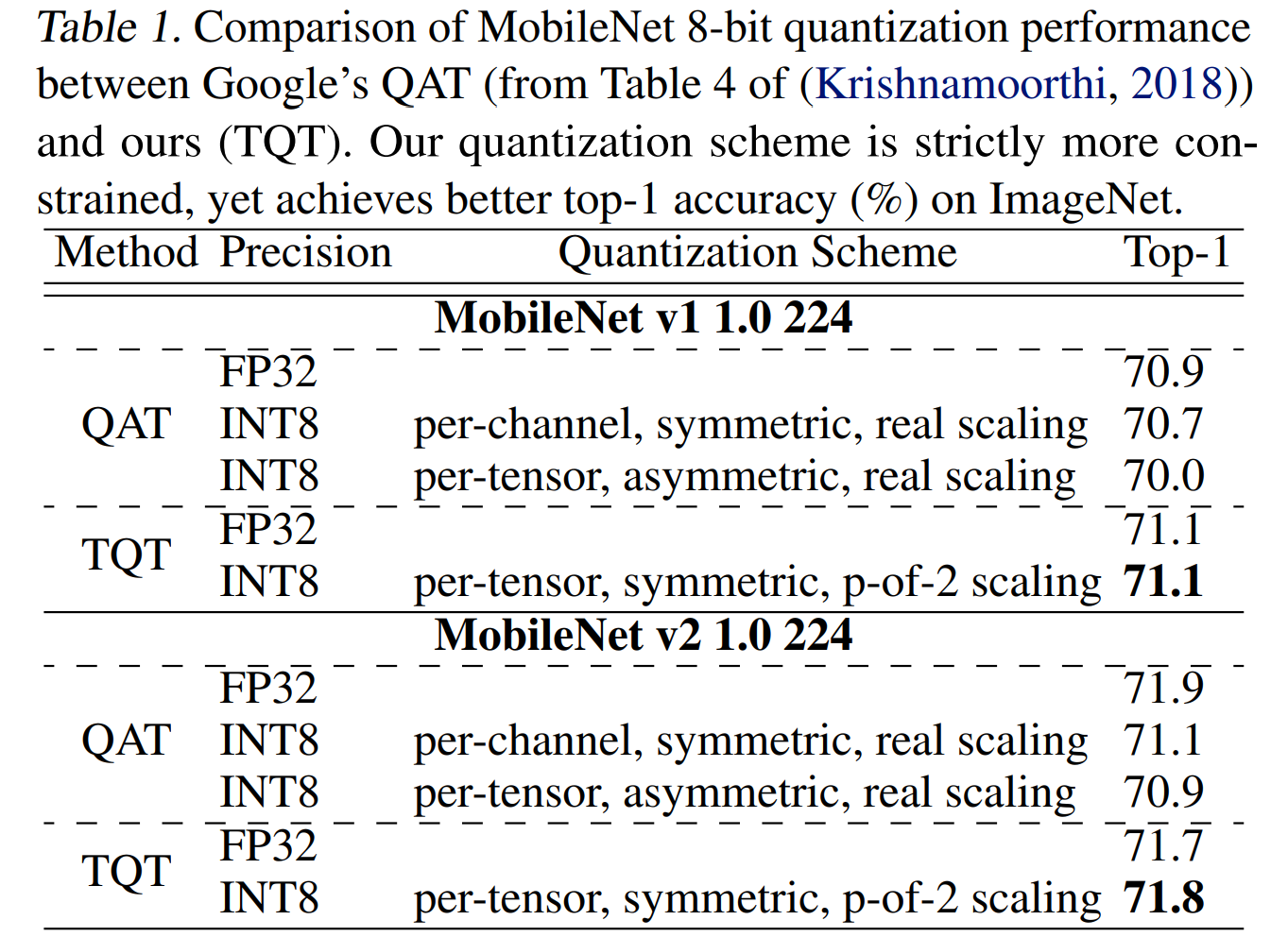Table 1
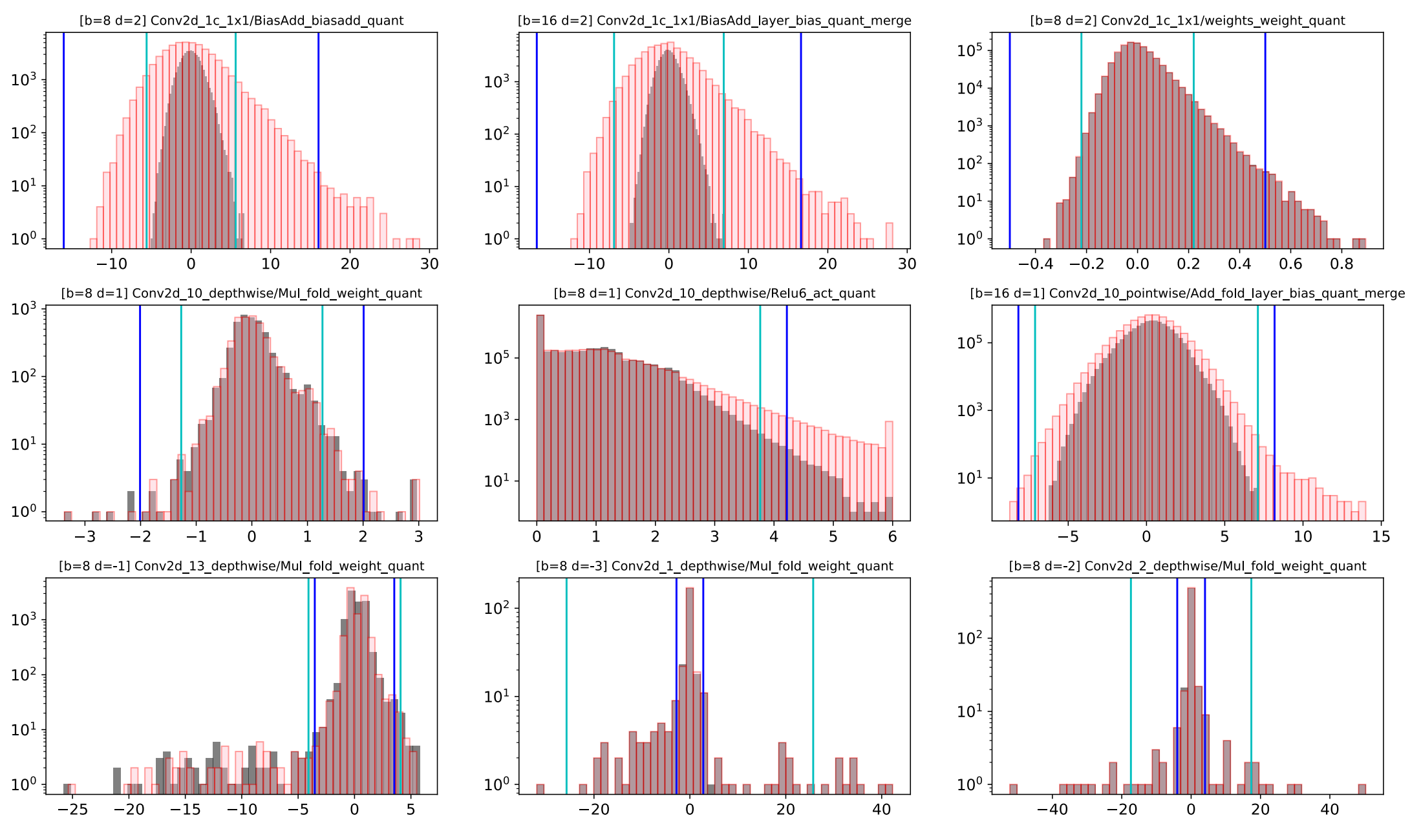Figure 5
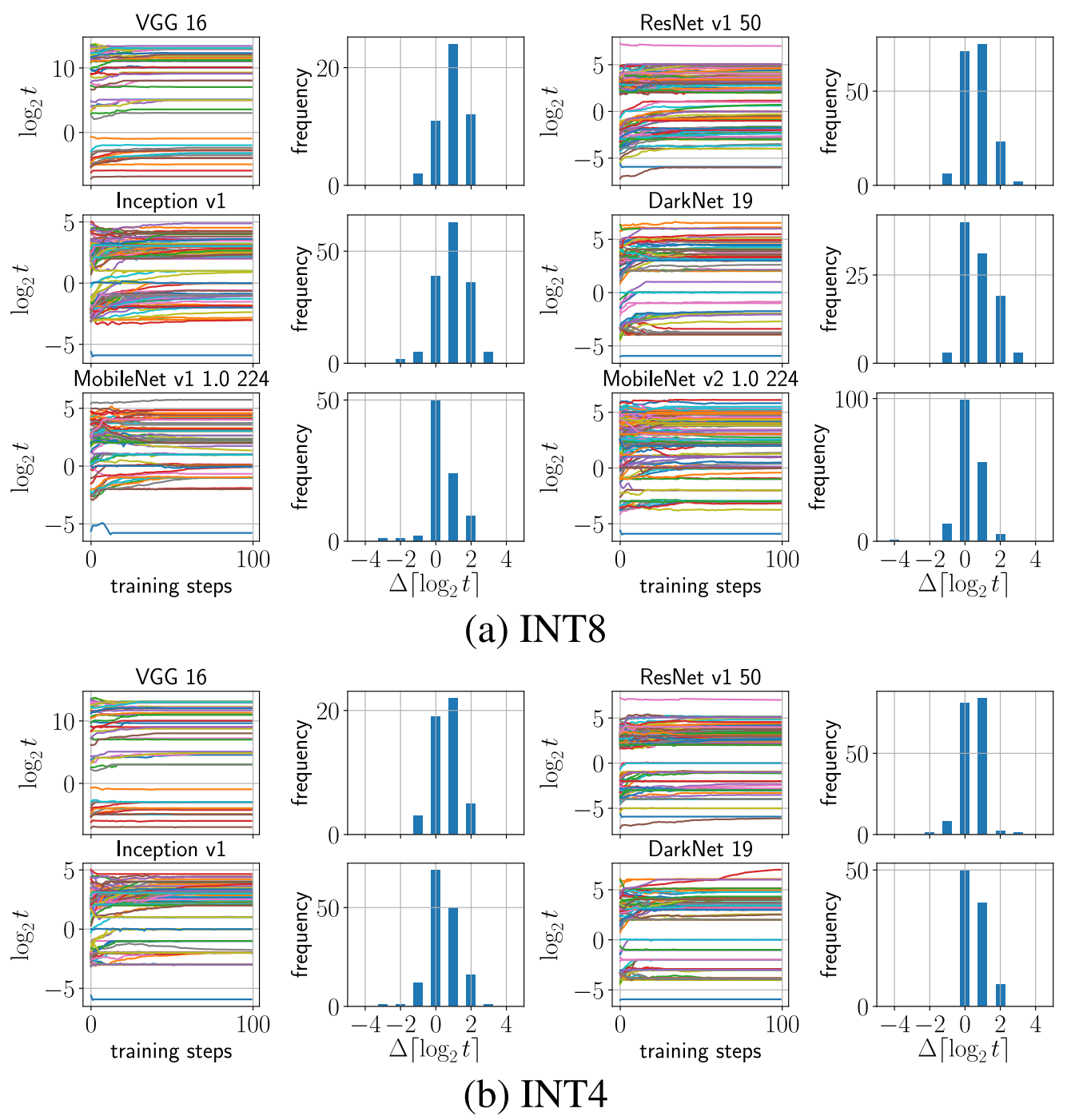Figure 6
Conclusion
本文提出了一种通用的学习量化截断阈值的方法 TQT。其特性如下：
- TQT 方法能够将量化步长限制在 PoT 型数值，适用于大多数支持定点运算的硬件。
- TQT 学习量化截断阈值的过程能够体现出截断范围和模型精度的 trade-off，并在 INT8 和 INT4 量化中取得很高的精度。
- TQT 方法具有鲁棒性和快速收敛性等特点。
此外，本文就 TQT 方法基于 TensorFlow 上建立了 Graffitist 项目，并基于 ImageNet 图像分类任务对多个经典模型进行量化实验，最后，本文就某些值得关注的实验现象进行阐述。
Appendices
本文的附录内容简单总结如下：
A Cost of Affine Quantizer
本节主要对量化器的计算开销进行分析讨论。
附录 A.1 对量化乘法运算进行详细分析，表明忽略量化零点 $Z$ 后可以有效地降低量化计算复杂度。
附录 A.2 分析了浮点型、dyadic 型和 PoT 型量化步长的乘法运算，其中dyadic型详见Google论文，PoT型可以直接使用移位运算代替乘法运算。
B Log Threshold Training
本节主要针对QAT过程进行分析，主要从数值稳定性、尺度不变性和收敛性三个方面进行讨论分析。
附录B.1分析训练的数值稳定性(Numeral Stability)。比起训练范围受限的原始截断阈值 $t \in \mathbb{R}^+$，不如直接训练 $\text{log} _2 \thinspace t \in \mathbb{R}$，并且 $\text{log}$ 函数的形式与PoT型正好吻合。
附录B.2分析训练的尺度不变性(Scale Invariance)，也就是说其梯度应该尽量与其取值大小无关，而只与其它因素有关。
附录B.3分析训练的收敛性(Convergence)，并给出了不同比特位下Adam优化器的参数取值参考。
C Adam Convergence
本节主要针对TQT在Adam优化器上的收敛性进行详细分析。
D Best or Mean Validation
本节主要针对该工作的实验结果筛选进行解释。本文在MobileNetV1和VGG16上的1000次验证平均准确率与最高准确率的差距分别为 $0.1\%$ 和 $0.2\%$，表明结果的真实性和可靠性。