MD5(Message Digest 5) 诞生于 1992 年,是对 MD4 算法的改进。作为目前使用最为普遍的加密哈希函数之一,MD5 自诞生起其安全性就被广泛研究。针对 MD5 最著名的攻击方式是 semi-free start collision,这种攻击方式将哈希函数的参数初始标准值替换为了其它的非标准值,从而实现了攻击。本文提出了一种针对 MD5 的攻击方式,该攻击能够在 $15$ 分钟到一个小时的计算时间内发现 MD5 碰撞。该攻击是一种差分攻击,但与大多数差分攻击不同,该攻击使用模整数减法代替异或作为差异度量,这种差分称为模差 (modular differential)。该攻击在 MD4 上可以在不到几分之一秒的时间内发现碰撞。此外,这种攻击也适用于 RIPEMD、HAVAL 等其他哈希函数。
- Title: How to Break MD5 and Other Hash Functions
- Venue: EUROCRYPT 2005
- Author(s): Xiaoyun Wang, Hongbo Yu
- Institution(s): Shandong University
- Link(s): Springer
1 Introduction
数字签名 (Digital Signatures) 在信息安全领域十分重要。数字签名的安全性取决于其底层实现的哈希函数的强度。哈希函数在密码学中还有如数据完整性 (Data Integrity)、分组签名 (Group Signature)、电子现金 (E-Cash) 等诸多应用。在这些应用中使用哈希函数不仅可以保证安全性,而且也能很大程度上提高效率。目国际通用的哈希函数有 MD5 和 SHA-1 两种。
MD5 是由 Ron Rivest 设计的哈希函数,是 MD4 的加强版。自 1992 年发布至今,研究者们已经逐渐发现了 MD5 的一些弱点。1993 年,B.den Boer 和 A. Bosselaers 发现了一种 MD5 的由两组相同信息和不同初始值产生的伪碰撞 (Pseudo-Collision)。这种攻击揭露了 MD5 中所有链接变量最高有效位的弱雪崩现象。在 Eurocrypt’96 的 Rump Session,H. Dobbertin 提出了一种 semi free-start collision 攻击,该攻击由两组不同的信息和给定的初始值 $IV_0’$ 组成。$IV_0’$ 取值为:
$$
a_0=\text{0x12ac2375},b_0=\text{0x3b341042},c_0=\text{0x5f62b97c},d_0=\text{0x4ba763ed}
$$
尽管 H. Dobbertin 的攻击方法并不能得到一个真正的 MD5 碰撞,但这种对 MD5 碰撞的攻击尝试揭露了 MD5 算法的弱雪崩现象。这也使在一次迭代中找到特殊形式的差分成为可能。
本文介绍将一种非常强大的寻找 MD5 碰撞的攻击方法。受 H. Dobbertin 的攻击方法的启发,我们对以下问题进行研究:是否有可能找到一对信息,每个信息由两个信息块组成,在经过这对信息的第二个信息块后能够产生 MD5 碰撞。具体来说,我们希望找到一对信息 $(M_0,M_1)$ 和 $(M_0’,M_1’)$ 使得:
$$
\begin{align}
& (a,b,c,d)=\text{MD5}(a_0,b_0,c_0,d_0,M_0), \\
& (a’,b’,c’,d’)=\text{MD5}(a_0,b_0,c_0,d_0,M_0’), \\
& \text{MD5}(a,b,c,d,M_1)=\text{MD5}(a’,b’,c’,d’,M_1’), \\
\end{align}
$$
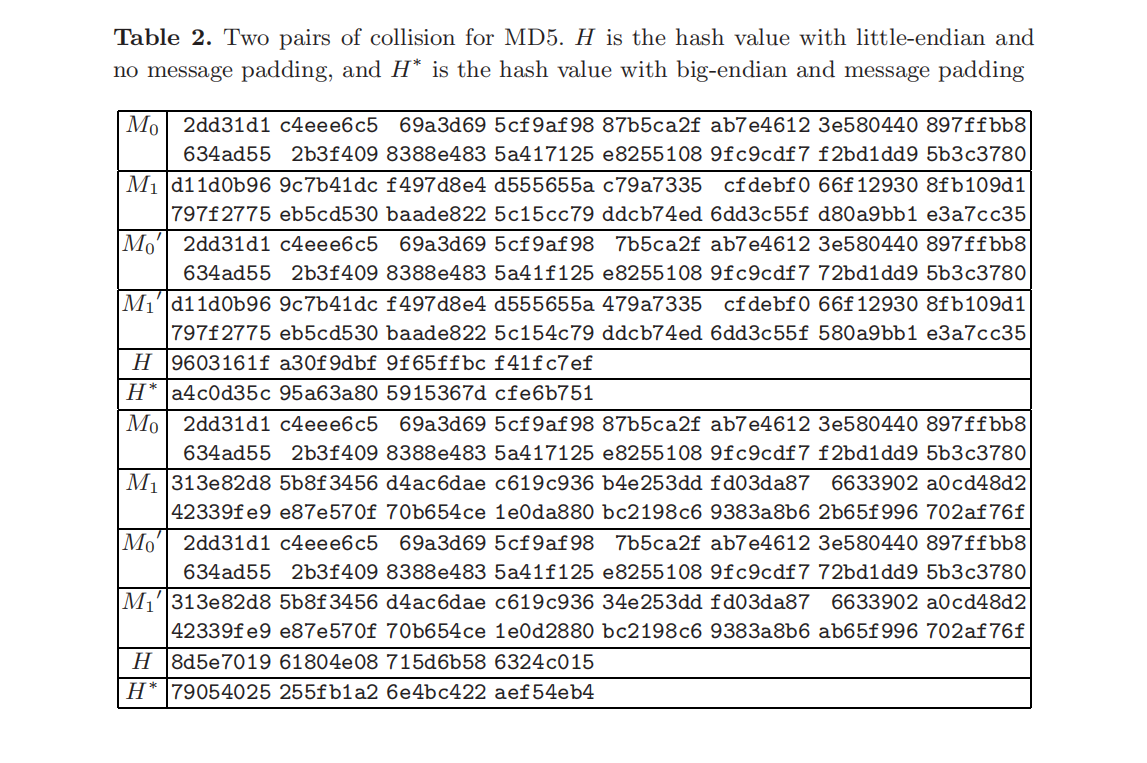
其中 $a_0,b_0,c_0,d_0$ 为 MD5 的初始值。以这种方式来寻找 MD5 碰撞比之前的方法效率更高:找到第一个信息块 $(M_0,M_0’)$ 大约需要 $2^{29}$ 次 MD5 运算,找到第二个信息块 $(M_1,M_1’)$ 大约需要 $2^{32}$ 次 MD5 运算。在一台 IBM P690 机器上应用这种攻击找到信息块 $M_0$ 和 $M_0’$ 需要大约一个小时,最快时只需要 $15$ 分钟。之后找到信息块 $M_1$ 和 $M_1’$ 只需要 $15$ 秒到 $5$ 分钟。应用这种攻击方式产生的两个 MD5 碰撞结果 (见表2) 已于 Crypto’04 大会的 Rump Session 中公布。
在 Crypto’04 大会上 Eli Biham 和 Rafi Chen 介绍了他们对 SHA-0 的近碰撞攻击方法,他们在大会的 Rump Session 中介绍了他们对 SHA-0 和 SHA-1 攻击的最新成果。A. Joux 介绍了对 SHA-0 的 $4$ 信息块完全碰撞攻击方法。
本文的组织结构如下:
- 第 2 部分简单介绍 MD5 算法;
- 第 3 部分介绍本文的攻击方法的主要思想;
- 第 4 部分对本文的攻击方法进行详细介绍;
- 第 5 部分对全文进行总结,并讨论本文的攻击方法对其它哈希函数的适用性。
2 Description of MD5
这里简单地介绍 MD5 算法的计算流程。
MD5 的哈希函数(Hash Function)。通常一个哈希函数是由一个压缩函数 $X=f(Z)$ 迭代若干次得到的。压缩函数能够将一个长度为 $l$ 比特位的信息块 $Z$ 转换为一个长度为 $s$ $(l<s)$ 比特位的哈希值 $X$,在 MD5 算法中,信息块长度 $l=512$, 哈希值长度 $s=128$。这种建立哈希函数的迭代式结构被称为 Merkle-Damgard 结构。对于一个经过填充补齐后比特位长度为 $512$ 倍数的信息 $M$,其迭代过程如下:
$$
H_{i+1}=f(H_i,M_i),\space 0 \leq i \leq t-1
$$
其中 $M=(M_0,M_2,\cdots,M_{t-1})$,迭代的初始值 $H_0=IV_0$。
由于本文提出的攻击方式的信息(两个信息块)长度已是 $512$ 的倍数,因此填充与否不影响攻击结果。
MD5 的压缩函数 (Compression Function)。信息 $M$ 的每个长度为 $512$ 比特位的信息块 $M_i$ 都等分为 $16$ 个长度为 $32$ 比特位的字 (Word) $M_i=(m_0,m_1,\cdots,m_{15})$,对于每一个信息块,压缩函数都会分 $4$ 个阶段(Round)执行,每个阶段进行 $16$ 步循环 (step operation),每连续 $4$ 步循环的操作如下:
$$
\begin{align}
& a=b+((a+\phi_i(b,c,d)+w_i+t_i)\lll s_i) \\
& d=a+((d+\phi_{i+1}(a,b,c)+w_{i+1}+t_{i+1})\lll s_{i+1}) \\
& c=d+((c+\phi_{i+2}(d,a,b)+w_{i+2}+t_{i+2})\lll s_{i+2}) \\
& b=c+((b+\phi_{i+3}(c,d,a)+w_{i+3}+t_{i+3})\lll s_{i+3}) \\
\end{align}
$$
其中运算符 $+$ 表示模 $2^{32}$ 加法运算。$t_{i+j}$ 和 $s_{i+j}$ $(j=0,1,2,3)$ 表示与循环步数相关的常数。$w_{i+j}$ 表示信息字。$\lll s_{i+j}$ 表示循环左移 $s_{i+j}$ 位。
每个阶段都会采用不同的非线性轮函数 (Non-linear Round Function),如下所示:
$$
\begin{align}
& \phi_i(X,Y,Z)=(X \land Y) \lor (\neg X \land Z), & 0 \leq i \leq 15, \\
& \phi_i(X,Y,Z)=(X \land Z) \lor (Y \land \neg Z), & 16 \leq i \leq 31, \\
& \phi_i(X,Y,Z)=X \oplus Y \oplus Z, & 32 \leq i \leq 47, \\
& \phi_i(X,Y,Z)=Y \oplus (X \lor \neg Z), & 48 \leq i \leq 63,\\
\end{align}
$$
其中 $X,Y,Z$ 均为长度为 $32$ 比特位的字。
MD5 的链接变量 (chaining variables)。MD5 的链接变量 $a,b,c,d$ 初始化如下:
$$
a=\text{0x67452301}, b=\text{0xefcdab89}, c=\text{0x98badcfe}, d=\text{0x10325476}
$$
逐字相加 (Wordwise Addition)。令 $H_{i-1}=(aa,bb,cc,dd)$ 为前一个信息块的链接变量,在经过 $4$ 个阶段之后,$H_{i-1}$ 与经过一次迭代后的链接变量进行逐字相加后得到压缩函数的输出值 $H_i$。
3 Differential Attack on MD5
3.1 The Modular Differential and the XOR Differential
差分攻击是针对哈希函数和分组密码最重要的分析方法之一。差分攻击,尤其是分组密码中的差分攻击,一般是一种以异或 (XOR) 作为差分的攻击方式。E. Biham 和 A. Shamir 使用差分攻击来分析类似 DES(Data Encryption Standard) 的加密系统的安全性,他们在其研究成果中称差分密码分析是一种分析明文对中的特定差异对生成的密文对差异的影响的方法。
本文对差分的定义是一种基于整数模减法运算差异的精确差分。本文还使用模特征来描述每个阶段的异或运算差异和整数模减法运算差异。两种差异的结合相比两者各自而言能够提供更多有价值的信息。
例如,对于某个未知量 $X$,当整数模减法运算值为 $X’-X=2^6$ 时,异或运算值有多种可能情况:
- 第 $7$ 位存在一个比特位的差异:异或运算值为 $\text{0x00000040}$。这种情况下 $X’$ 和 $X$ 的第 $7$ 位分别是 $1$ 和 $0$;
- 存在两个比特位的差异:即减法运算时存在第 $7$ 位向第 $8$ 位借位,异或运算值为 $\text{0x000000c0}$。这种情况下 $X’$ 和 $X$ 的第 $7$、$8$ 位分别是 $10$ 和 $01$;
- 存在三个比特位的差异:即减法运算时存在第 $7$ 位向第 $8$ 位再向第 $9$ 位借位,异或运算值为 $\text{0x000001c0}$。这种情况下 $X’$ 和 $X$ 的第 $7$、$8$、$9$ 位分别是 $100$ 和 $011$;
- 存在更多比特位的差异:与前面类似,减法运算时存在更多连续的借位,$X’$ 和 $X$ 的二进制形式分别如 $1000\dots$ 和 $0111\dots$;
- 假如整数模减法的运算值为负值,异或运算值仍然相同,$X’$ 和 $X$ 的取值与上述情况相反,即 $X’$ 和 $X$ 的二进制形式分别如 $0001\dots$ 和 $1110\dots$。
为了能够更加清楚地解释本文的攻击方式,本文在表示模差异时结合了其它两种差异,即使用一个正或负整数(对 $2^{32}$ 取模)和异或差异来同时表示。其中异或差异由一个由比特位和其对应的符号所组成元素的序列来表示。序列中 $X$ 对应位的值为 $0$ 标记为无符号,$X$ 对应位的值为 $1$ 标记为负号。例如,对于模减法运算的差 $-2^6$,$[7,8,9,\cdots,22,-23]$ 表示从第 $7$ 位直到 $23$ 位借位的模减法运算的差 $X’-X=-2^6 \space (X’<X)$,$X$ 的第 $7$ 到 $22$ 位全部为 $0$,第 $23$ 位为 $1$ ;$X’$ 的第 $7$ 到 $22$ 位全部为 $1$ ,第 $23$ 位为 $0$ 。一个更复杂的例子是 $-1-2^6+2^{23}-2^{27}$,$[1,2,3,4,5,-6,7,8,9,10,11,-12,-24,-25,-26,27,28,29,30,31,-32]$,其中的模减法运算的差由多个 $2$ 的指数(可正可负)幂组成,异或差异根据不同借位则会有多种不同的值。需要注意在模减法运算中,最高位即第 $32$ 位符号位也能够被借位,借位后第 $32$ 位没有负号。
值得一提的是,之前的一些研究也已经使用模差来对 SHA-0、MD4、RIPEMD 等哈希函数进行分析。但与之前的研究相比,本文设计的攻击方式有以下几点优势:
- 寻找的信息只包含两个 $512$ 位的信息块,因此该攻击能够在两次迭代后产生碰撞;
- 该攻击是一种精确的差分攻击,其特征比使用时更加严格,并且该攻击除了给出差异之外,还能给出具体比特位的值;
- 该攻击给出了一组能够确保差分产生的充分条件;
- 该攻击使用了一种信息修改技术(Message Modification Technique),能够大幅提高碰撞发生的概率。
3.2 Differential Attacks on Hash Functions
两个参数 $X$ 和 $X’$ 的差异(Difference)定义为 $\varDelta X=X’-X$。对于任意两个长度为 $l$ 且为 $512$ 倍数的信息 $M$ 和 $M’$,$M=(M_0,M_1,\cdots,M_{k-1})$, $M’=({M_0}’,{M_1}’,\cdots,{M_{k-1}}’)$,哈希函数的完全差分 (Differential) 定义如下:
$$
\varDelta H_0 \stackrel{(M_0,M_0’)}{\longrightarrow}
\varDelta H_1 \stackrel{(M_1,M_1’)}{\longrightarrow}
\varDelta H_2 \stackrel{(M_2,M_2’)}{\longrightarrow}
\cdots\cdots
\varDelta H_{k-1} \stackrel{(M_{k-1},M_{k-1}’)}{\longrightarrow}
\varDelta H,
$$
其中 $\varDelta H_0$ 为初始的差异值,初值为零。$\varDelta H$ 为两信息的输出差异值。$\varDelta H_i = \varDelta IV_i$ 为第 $i$ 次迭代的输出差异值以及下一次迭代的初始值。
显然,如果 $\varDelta H=0$,则 $M$ 和 $M’$ 之间发生了碰撞。能够产生碰撞的差分称为碰撞差分 (Collision Differential)。
已知 MD5 的哈希函数有 $4$ 个阶段,每个阶段进行 $16$ 步循环操作,对于第 $i$ 次迭代的差分 $\varDelta H_i \stackrel{(M_i,M_i’)}{\longrightarrow} \varDelta H_{i+1}$,可展开为如下形式:
$$
\varDelta H_1 \stackrel{P_1}{\longrightarrow}
\varDelta R_{i+1,1} \stackrel{P_2}{\longrightarrow}
\varDelta R_{i+1,3} \stackrel{P_3}{\longrightarrow}
\varDelta R_{i+1,1} \stackrel{P_4}{\longrightarrow}
\varDelta R_{i+1,4}=\varDelta H_{i+1}
$$
各阶段差分变化 $\varDelta R_{j-1} \longrightarrow \varDelta R_j (j=1,2,3,4)$ 及其概率 $P_j$ 可展开为如下差分特征(Differential Characteristics):
$$
\varDelta R_{j-1} \stackrel{P_{j1}}{\longrightarrow}
\varDelta X_i \stackrel{P_{j2}}{\longrightarrow}
\cdots\cdots \stackrel{P_{j16}}{\longrightarrow}
\varDelta X_{16} = \varDelta R_j
$$
其中 $\varDelta X_{t-1} \stackrel{P_{jt}}{\longrightarrow} \varDelta X_t, t=1,2,\cdots\cdots,16$ 是第 $j$ 阶段中第 $t$ 个循环的差分特征。
一次迭代的差分 $\varDelta H_i \stackrel{(M_i,M_i’)}{\longrightarrow} \varDelta H_{i+1}$ 的概率 $P$ 满足:
$$
P \geq \prod_{i=1}^4 P_j \space\text{and}\space P_j \geq \prod_{t=1}^{16} P_{jt}.
$$
3.3 Optimized Collision Differentials for Hash Functions
在 3.1 节提到,本文的攻击方法采用了一种信息修改技术来提高碰撞发生的概率。根据这种修改技术,可以得到一个粗略的方法来寻找一个更优的哈希函数的差分(包括碰撞差分)。
信息修改的方式有两种:
对任意两个信息块 $(M_i, M_i’)$ 和第一阶段的非零差分
$$
\varDelta H_i \stackrel{(M_i,M_i’)}{\longrightarrow}
\varDelta R_{i+1,1}.
$$
本文的攻击方法可以很容易地修改信息块 $M_i$ 以保证第一阶段的差分发生的概率 $P_1=1$。采用多重信息修改技术,不仅可以保证第一阶段的差分的概率保持为 $1$,而且还能大大提高第二阶段的差分的概率。
要想找到更优的哈希函数的差分,最好选定一个信息块差异,使其能够在之后两阶段差分仍然有很高的概率发生。
4 Differential Attack on MD5
4.1 Notation
为了简化讨论,在正式介绍本文的攻击方法之前,首先引入如下数学表示:
- $M=(m_0,m_1,\cdots,m_{15})$ 以及 $M’=(m_0’,m_1’,\cdots,m_{15}’)$ 分别表示两个长度为 $512$ 个比特位数的信息块。$\varDelta M = (\varDelta m_0,\varDelta m_1,\cdots,\varDelta m_{15})$ 表示两个信息块的差异。其中 $\varDelta m_i=m_i’-m_i$ 为第 $i$ 个字的差异。
- $a_i,b_i,c_i,d_i$ 分别表示第 $4i-3,4i-2,4i-1,4i$ 步循环中压缩函数的输出,其中 $1 \leq i \leq 16$。$a_i’,b_i’,c_i’,d_i’$ 的定义与1类似;
- $a_{i,j},b_{i,j},c_{i,j},d_{i,j}$ 分别表示 $a_i,b_i,c_i,d_i$ 的第 $j$ 位,其中第 $1$ 位为最低有效位,第 $32$ 位为最高有效位。
- $\phi_{i,j}$ 为第 $i$ 步循环操作中的非线性轮函数 $\phi$ 输出值的第 $j$ 位。
- $\varDelta x_{i,j}=x_{i,j}’-x_{i,j}=\pm 1$ 表示改变 $x_i$ 的第 $j$ 位之后产生的位差。$x_i[j],x_i[-j]$ ($x$ 可以是 $a,b,c,d,\phi$) 是只改变字 $x_i$ 中第 $j$ 位之后的取值。$x_i[j]$ 由 $x_i$ 的第 $j$ 位从 $0$ 变到 $1$ 时得到,$x_i[-j]$ 由 $x_i$ 的第 $j$ 位从 $1$ 变到 $0$ 时得到。
- $\varDelta x_i[j_1,j_2,\cdots,j_l]=x_i[j_1,j_2,\cdots,j_l]-x_i$ 表示 $x_i$ 的第 $j_1,j_2,\cdots,j_l$ 位变化时产生的差异。$x_i[\pm j_1, \pm j_2,\cdots,\pm j_l]$ 由 $x_i$ 的第 $j_1,j_2,\cdots,j_l$ 位变化得到。$+$ 号(一般可忽略)指当前位的值从 $0$ 变为 $1$,$-$ 号指当前位的值从 $1$ 变为 $0$。
4.2 Collision Differentials for MD5
本文的攻击可以使用 MD5 原本的初始值 $IV_0$ 来寻找不同的由两个长度 $1024$ 位的信息 $M_0,M_1$ 和 $(M_0’,M_1’)$ 产生的碰撞。攻击中的两次迭代产生的碰撞差分如下:
$$
\varDelta H_0 \stackrel{(M_0,M_0’)}{\longrightarrow}
\varDelta H_1 \stackrel{(M_1,M_1’)}{\longrightarrow}
\varDelta H=0
$$
其中
$$
\begin{align}
& \varDelta M_0=M_0’-M_0=(0,0,0,0,2^{31},0,0,0,0,0,0,2^{15},0,0,2^{31},0) \\
& \varDelta M_1=M_1’-M_1=(0,0,0,0,2^{31},0,0,0,0,0,0,-2^{15},0,0,2^{31},0) \\
& \varDelta H_1=(2^{31},2^{31}+2^{25},2^{31}+2^{25},2^{31}+2^{25}) \\
\end{align}
$$
$M_0$ 和 $M_1$ 的非零项分别在第 $5$、$12$、$15$ 个字(从高往低)。$\varDelta H_1=(\varDelta a,\varDelta b,\varDelta c,\varDelta d)$ 为四个链接变量 $(a,b,c,d)$ 在第一次迭代后产生的差异。
$\varDelta M_0$ 需要保证第 $3$ 和 $4$ 阶段的差分以较高概率出现,$\varDelta M_1$ 不仅需要保证第 $3$ 和 $4$ 阶段的以较高概率出现差分,而且还要使产生的输出差异能够被输出差异 $\varDelta H_1$ 抵消。
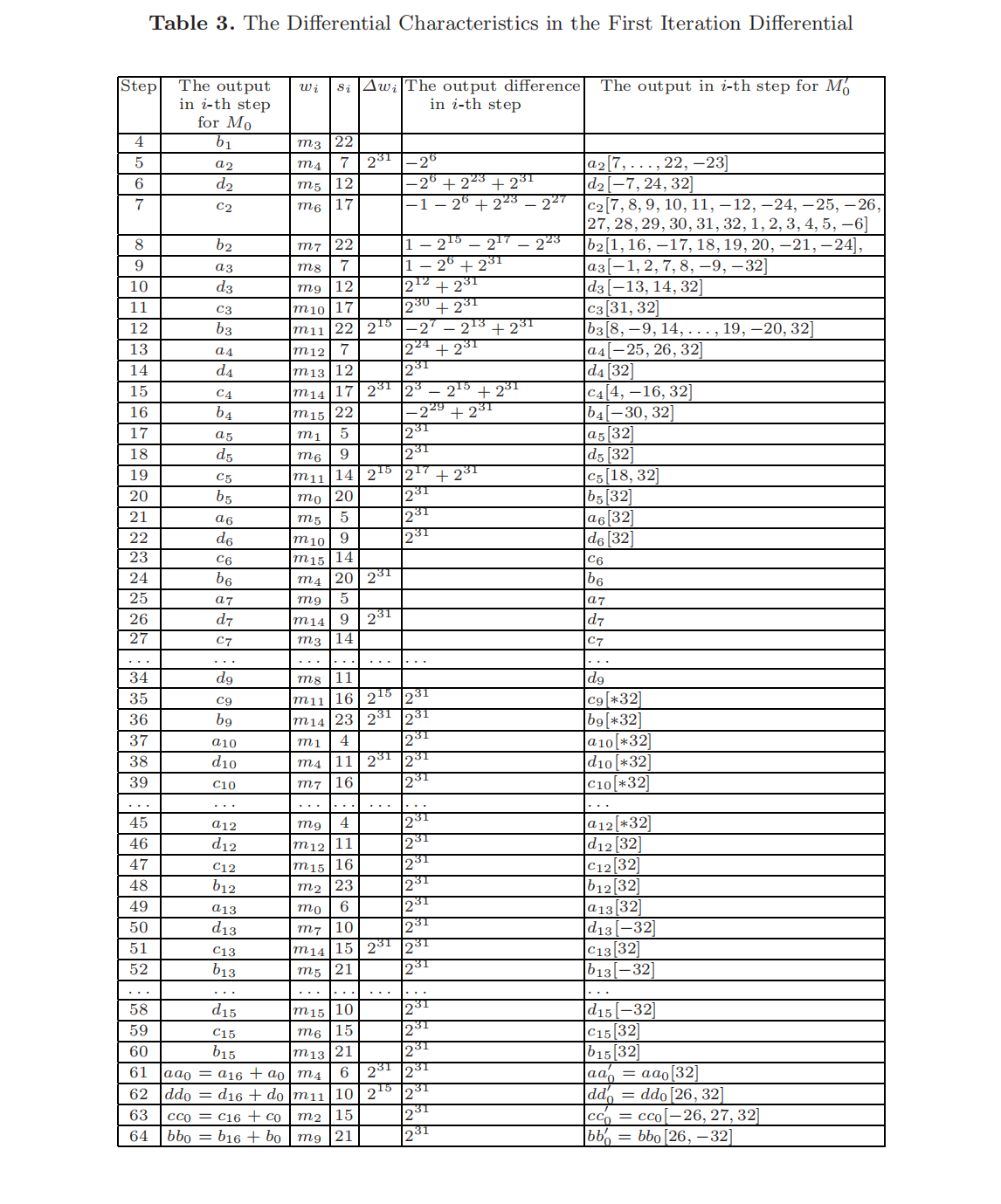
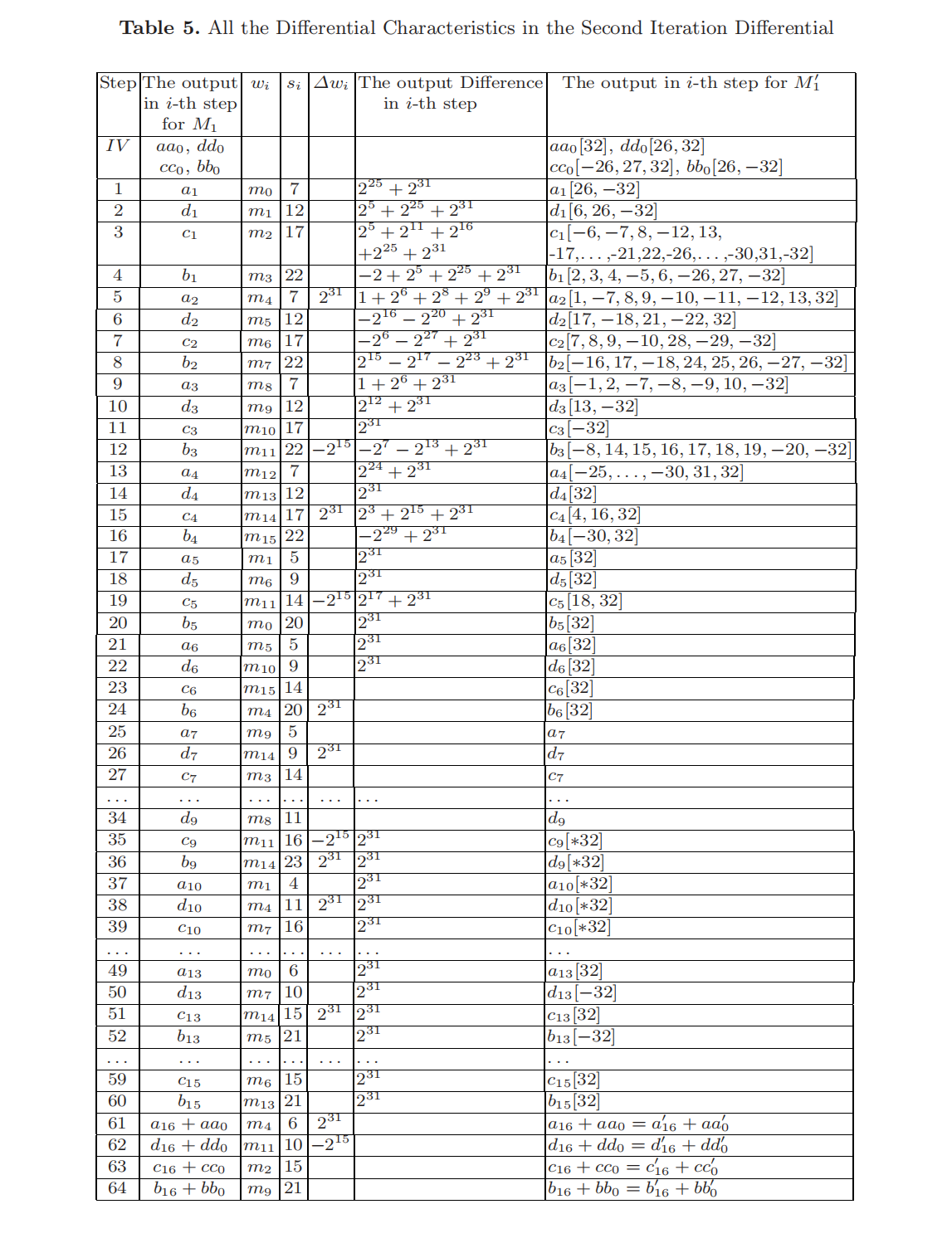
碰撞差分的所有差分特征见表 3 和表 5。两个表的所有列表示的含义相同。这里仅对表 3 进行解释。
- 第 1 列表示循环步数;
- 第 2 列表示处理第一个信息块 $M_0$ 时的每步循环中链接变量的值;
- 第 3 列表示处理第一个信息块 $M_0$ 时每步循环中的信息字;
- 第 4 列表示每步循环中的循环左移的位数;
- 第 5、6 列分别表示 $M_0$ 和 $M_0’$ 的信息字和链接变量之间的差异;
- 第 7 列表示 $M_0’$ 的链接变量值。
表中第 6、7 列中的空白项代表信息字或链接变量之间没有差异。信息字和链接变量两者均不存在差异的循环步没有在表中列出。
4.3 Sufficient Conditions for the Characteristics to Hold
接下来给出如何推导得到一组能够保证在 MD5 的第 $8$ 步循环(表3)中差分特征成立的充分条件的一个具体例子。其它的充分条件可以类似地推导给出。
MD5的第 $8$ 步循环中的差分特征为:
$$
(\varDelta c_2,\varDelta d_2,\varDelta a_2,\varDelta b_1,) \longrightarrow \varDelta b_2.
$$
其中每个链接变量满足下列等式关系:
$$
\begin{align}
& b_1’=b_1 \\
& a_2’=a_2[7,\cdots,22,-23] \\
& d_2’=d_2[-7,24,32] \\
& c_2’=c_2[7,8,9,10,11,-12,-24,-25,-26,27,28,29,30,31,32,1,2,3,4,5,-6] \\
& b_2’=b_2[1,16,-17,18,19,20,-21,-24] \\
\end{align}
$$
根据第 $8$ 步循环的压缩函数,可得:
$$
\begin{align}
& b_2=c_2+((b_1+F(c_2,d_2,a_2)+m_7+t_7)\lll 22 \\
& b_2’=c_2’+((b_1+F(c_2’,d_2’,a_2’)+m_7’+t_7)\lll 22 \\
& \phi_7=F(c_2,d_2,a_2)=(c_2 \land d_2) \lor (\neg c_2 \land a_2) \\
\end{align}
$$
在上面的压缩函数的操作中,$c_2$ 在等式右端项中出现了两次,为了加以区分,不妨令 $c_2^F$ 指代函数 $F$ 内的 $c_2$,$c_2^{NF}$ 指代函数 $F$ 外的 $c_2$。
本推导过程基于以下两个事实:
- 由 $\varDelta b_1=0$ 且 $\varDelta m_7=0$,可知 $\varDelta b_2=\varDelta c_2^{NF}+(\varDelta \phi_7 \lll 22$);
- 固定函数 $F$ 中的一或两个参数后,可以使函数 $F$ 退化为单一变量函数。
基于上述条件,可以得到一组保证差分特征不变的充分条件。以下根据 $\varDelta b_2$ 不同位的取值情况来分别讨论:
- $\varDelta b_2$ 中非零位的情况
$\text{(a)}$ $d_{2,11}=1, b_{2,1}=0$ 的情况下,可以保证 $b_2$ 的第一位发生变化。
$\text{i}.$ 若 $d_{2,11}=\overline{a_{2,11}}=1$,可知 $\varDelta \phi_{7,11}=1$;
$\text{ii}.$ 执行 $\lll 22$ 循环左移操作之后,$\varDelta \phi_{7,11}$ 在第 $1$ 位;
$\text{iii}.$ 由于 $\varDelta c_{2,1}^{NF}=0$,故 $\varDelta b_{2,1}=\varDelta c_{2,1}^{NF} + \varDelta \phi_{7,11}=1$。
$\text{(b)}$ $d_{2,26}=\overline{a_{2,26}}=1,b_{2,16}=0$ 且 $b_{2,17}=1$ 的情况下,可以保证 $b_2$ 的第 $16$、$17$ 位发生变化;
$\text{(c)}$ $d_{2,28}=\overline{a_{2,28}}=0,b_{2,i}=0,i=18,19,20$ 且 $b_{2,21}=1$ 可以保证 $b_2$ 的第 $18$、$19$、$20$、$21$ 位发生变化;
$\text{(d)}$ $d_{2,3}=\overline{a_{2,3}}=0,b_{2,24}=1$ 的情况下,可以保证 $b_2$ 的第 $24$ 位发生变化。可以通过下式证明:
$$
\varDelta c_2^{NF}[-24,-25,-26,27]+(\varDelta \phi_7[3] \lll 22)=2^{23}-2^{24}=-2^{23}.
$$
$\varDelta b_2$ 中零位的情况
$\text{(a)}$ 当 $c_{2,17}=0$ 时,可以保证 ${c_2’}^{NF}$ 的第 $7$、$12$ 位和 $a_2’$ 的第 $17$ 位发生变化,且 $b_2$ 保持不变。可以通过下式简单地进行证明:
$$
\varDelta c_2^{NF}[7,\cdots,11,-12]+(\varDelta \phi_7[17] \lll 22)=-2^6+2^6=0.
$$
$\text{(b)}$ 当 $d_{2,i}=a_{2,i}$ 时,可以保证 $c_2^F$ 的第 $i$ 为发生变化,且 $b_2$ 保持不变,其中 $i \in {1,2,4,5,25,27,29,30,31}$;
$\text{(c)}$ 当 $c_{2,i}=1$ 时,可以保证 $a_2$ 的第 $i$ 位发生变化,且 $b_2$ 保持不变,其中 $i \in {13,14,15,16,18,19,20,21,22,23}$;
$\text{(d)}$ 当 $d_{2,6}=\overline{a_{2,6}}=0$ 时,可以保证 $c_2^F$ 的第 $6$ 位发生变化,且 $b_2$ 保持不变;
$\text{(e)}$ 当 $a_{2,32}=1$ 时,可以保证 $c_2^F$ 和 $d_2$ 的第 $32$ 位发生变化,且 $b_2$ 保持不变;
$\text{(f)}$ 当 $d_{2,i}=0$ 时,可以保证 $a_2$ 和 $c_2^F$ 的第 $i$ 位发生变化,且 $b_2$ 保持不变,其中 $i \in {8,9,10}$;
$\text{(g)}$ 当 $d_{2,12}=1$ 时,可以保证 $a_2$ 和 $c_2^F$ 的第 $12$ 位发生变化,且 $b_2$ 保持不变;
$\text{(h)}$ 当 $a_{2,24}=0$ 时,可以保证 $c_2^F$ 和 $d_2$ 的第 $24$ 位发生变化,且 $b_2$ 保持不变;
$\text{(i)}$ 当 $c_2^F,d_2,a_2$ 的第 $7$ 位发生变化时,$b_2$ 保持不变。
通过类似的方法,可以得出一组充分条件来保证碰撞差分中的所有差分特征均保持不变。
4.4 Message Modification
单一信息修改 (Single-message Modification)。为了使攻击更加高效,可以通过固定一些信息字来提前满足一些充分条件,从而对本文的攻击方法加以改进。经过观察发现,很容易就能够生成满足 MD5 前 $16$ 步循环的条件的信息。
对于每个信息块 $M_0$ (或 $M_1$) 和中间值 ($H_0$ 或第二个信息块的 $H_1$ 和 $H_1’$),可以采用以下流程来对 $M_0$ (或相应的 $M_1$) 进行修改,使得表 4 和表 6 中的第一阶段 (前 $16$ 步循环) 的条件成立。很容易修改 $M_0$ 使得表 4 中第一阶段的条件成立的概率达到 $1$。
例如,为了确保表 4 中 $c_1$ 的 $3$ 个条件成立,可以将 $M_0$ 中的 $m_2$ 修改如下:
$$
c_1^{new} \longleftarrow c_1^{old}-c_{1,7}^{old} \cdot 2^6-c_{1,12}^{old} \cdot 2^{11}-c_{1,20}^{old} \cdot 2^{19}
$$
$$
m_2^{new} \longleftarrow ((c_1^{new}-c_1^{old}) \ggg 17)+m_2^{old}.
$$
通过对 $M_0$ 的每个信息字进行修改,表4中第一阶段的所有条件都能够成立。第一次迭代的差分成立的概率为 $2^{-43}$。
使用相同的方法也可以对 $M_1$ 进行修改。修改之后,第二次迭代的差分成立的概率为 $2^{-37}$。
多重信息修改(Multi-message Modification)。进一步观察发现,通过进行多重信息修改甚至有可能使某些前 $32$ 步循环的充分条件得到满足。
例如,如果 $a_{5,32}=1$,可以通过修改 $m_1,m_2,m_3,m_4,m_5$ 来将其修正为 $a_{5,32}=0$,以致在 $2$ 到 $6$ 步循环中生成一个局部碰撞,同时保持第一阶段的所有条件仍然成立,见表 1 。其它的条件也可以通过类似的修改方式或其它更加精确的修改方法来进行修正。使用这种修改方法后,表 4 的第 $2$ 到第 $4$ 阶段中还剩 $37$ 个条件未被确定,表6中的第 $2$ 到第 $4$ 阶段中还剩 $30$ 个条件未被确定。因此,第一次迭代差分出现的概率为 $2^{-37}$,第二次迭代差分出现的概率为 $2^{-30}$。
4.5 The Differential Attack on MD5
根据以上内容,易得本文对 MD5 的攻击方法。接下来将详细介绍如何找到如下形式的两个信息块产生的碰撞。
$$
\varDelta H_0 \stackrel{(M_0,M_0’),2^{-37}}{\longrightarrow}
\varDelta H_1 \stackrel{(M_1,M_1’),2^{-30}}{\longrightarrow}
\varDelta H=0
$$
重复以下步骤,直到找到第一个信息块 $M_0$:
$\text{(a)}$ 随机初始化一个信息 $M_0$;
$\text{(b)}$ 使用前面所述的信息修改技术对 $M_0$ 进行修改;
$\text{(c)}$ 然后,使用 $M_0$ 和 $M_0’=M_0+ \varDelta M_0$ 产生第一次迭代的差分
$$
\varDelta M_0 \longrightarrow (\varDelta H_1, \varDelta M_1)
$$
其出现概率为 $2^{-37}$;
$\text{(d)}$ 将 $M_0$ 和 $M_0’$ 代入压缩函数,检验是否所有差分特征全部成立。重复以下步骤,直到产生一个碰撞:
$\text{(a)}$ 随机初始化一个信息 $M_1$;
$\text{(b)}$ 使用前面所述的信息修改技术对 $M_1$ 进行修改;
$\text{(c)}$ 然后,使用 $M_1$ 和 $M_1+ \varDelta M_1$ 产生第二次迭代的差分
$$
(\varDelta H_1, \varDelta M_1) \longrightarrow \varDelta H=0
$$
其出现概率为 $2^{-30}$;
$\text{(d)}$ 检验这一对信息是否能够导致碰撞。
寻找 $(M_0,M_0’)$ 的复杂度不超过运行 $2^{39}$ 次 MD5 运算的时间。得到另一个信息 $M_0’$ 只需要更改之前 $M_0$ 的最后两个字。因此,寻找 $(M_0,M_0’)$ 只需要进行一次对 $M_0$ 的前 $14$ 个字的单一信息修改即可,时间消耗可以忽略不计。对于每一个选定的信息 $M_0$,只需要对最后 $2$ 个字进行 $2$ 次单一信息修改,以及在第二阶段中进行 $7$ 次多重信息修改分别对 $7$ 个条件进行修正,每次多重信息修改只需要很少的操作步骤。因此对于每一个选定的消息,所有两种修改的所用的总时间不超过两次 MD5 运算的时间。
根据第一次迭代差分的概率易知,该攻击方法中寻找 $(M_0,M_0’)$ 的复杂度不超过 $2^{39}$ 次 MD5 操作的时间。
表 2 给出了两个 MD5 碰撞的例子。需要注意的是,两个碰撞的第一个 $512$ 位信息块完全相同,并且当给定的第一个信息块满足所有的攻击标准时,很容易就能找到能够产生碰撞的第二个信息块 $(M_1,M_1’)$。
5 Summary
本文介绍了一种十分强大的哈希函数攻击方法,并表明使用该方法来寻找MD5碰撞是很容易实现的。该攻击同时也能够有效地破解如 HAVAL-128、MD4、RIPEMD 和 SHA-0 等哈希函数,具体分析结果如下:
- 寻找 MD4 碰撞的时间复杂度:不使用多重信息修改大约需要 $2^{23}$ 次MD4运算,使用多重信息修改大约需要 $2^8$ 次 MD4 运算。
- 寻找 HAVAL-128 碰撞的时间复杂度:不使用多重信息修改大约需要 $2^{13}$ 次HAVAL-128运算,使用多重信息修改大约需要 $2^7$ 次 HAVAL-128 运算。
- 寻找 RIPEMD 碰撞的时间复杂度:不使用多重信息修改大约需要 $2^{30}$ 次 RIPEMD 运算,使用多重信息修改大约需要 $2^{18}$ 次 RIPEMD 运算。
- 寻找 SHA-0 碰撞的时间复杂度:不使用多重信息修改大约需要 $2^{61}$ 次 SHA-0 运算,使用多重信息修改大约需要 $2^{45}$ 次 SHA-0 运算。