个人论文阅读报告留档
引言
问题背景
2012 年，AlexNet 在 ILSVRC 比赛上大放异彩，人工智能也随之走入了以深度学习技术为主的新的发展时期。在之后的几年里，基于深度学习的算法或模型在任务上的性能改进都与模型的参数量成正相关。复杂的模型的计算时间和空间复杂度都很高，在资源受限的硬件上部署仍然具有很大挑战。
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
神经网络量化的基本概念
量化
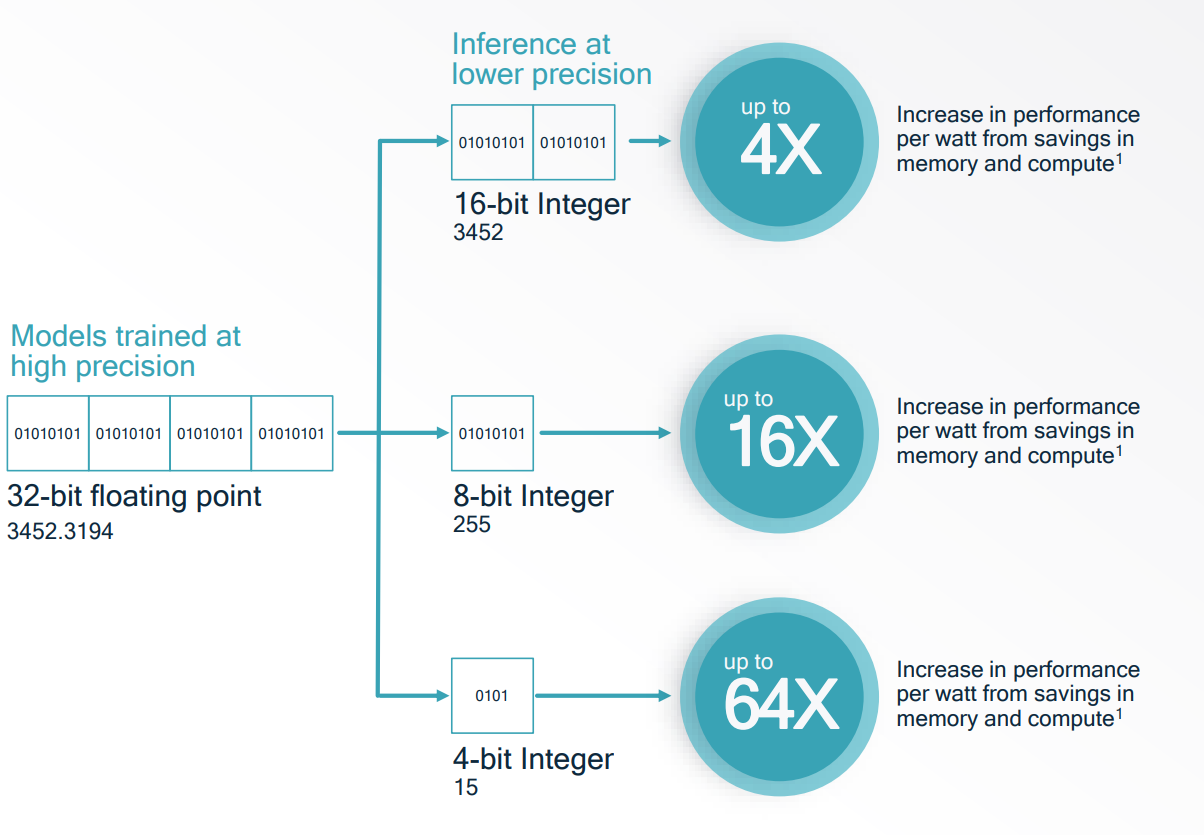
量化（Quantization）这一概念源自通信和信息学领域，是指一种从大（通常是连续）范围的输入值映射到（通常是离散）范围的输出值的方法。在数值计算问题中，量化问题指一组连续的实数值应该如何映射到一组取值固定的离散数值集合上，从而能够最大限度地减少数值表示所需的位数并最大限度地提高计算的精度。近年来，由于基于深度学习的神经网络模型的复杂度不断提高，对神经网络的量化问题的研究逐渐成为人工智能技术应用和神经网络计算优化的重要子领域。
针对深度神经网络的量化一般有两个目的：网络压缩和推理加速。网络压缩指通过降低模型参数（包括权重和激活值）的数值表示所需的位数，达到降低内存容量和带宽的效果，例如将一个参数全部是 32 位浮点数的神经网络的权重和激活值全部量化到 8 位整型数值，其内存占用和带宽理论上均可减少至原来的四分之一。而实现推理加速则是利用量化从高精度映射到低精度数值表示的特性，进行进一步的低精度（如整型）的计算优化，减少模型计算推理的时间，例如对 8 位整型数的乘法运算进行优化，可以理论上实现相比 32 位浮点数的乘法运算的速度快 16 倍的加速效果。
量化时的浮点数离散化操作会造成精度损失，因此在量化操作之后得到的值会与原真实值存在差异，这个差异叫作量化误差（Quantization Error）。直观上来说，将全精度的数值映射为低精度的数值会不可避免地导致信息丢失，这个过程中会对神经网络模型引入量化误差，导致模型预测精度的下降。但是实际上许多量化神经网络的表现与原始神经网络相差无几。关于量化误差与模型预测精度的相关性，目前尚未出现严谨的理论证明。一个可能的解释是：当前多数神经网络模型都存在严重的参数冗余，模型参数的自由度较高，因此对于参数的量化具有较高的鲁棒性。
{: width=”60%” loading=”lazy” style=”margin-bottom: 30px;”}
量化的数学表示
量化可以表示为一个单射函数 $Q$，该函数将输入的浮点数值集合 $X$ 映射到离散的数值集合 $Y$。函数 $Q$ 在过去的研究中有多种实现方式，其中使用得最为广泛的是对称仿射量化（Symmetric Affine Quantization），或者叫作对称线性量化（Symmetric Linear Quantization）。对称线性量化的一般形式如下：
$$
\begin{align*}
&Q(\mathbf{x}) = \text{clip}\left(\text{round}\left(\frac{\mathbf{x}}{s}\right)\right)\\
&\hat{\mathbf{x}} = s \cdot Q(\mathbf{x})
\end{align*}
$$
对于某一粒度规模（Layer-wise 或者 Channel-wise）的参数，对称线性量化使用一个缩放系数 $s$ 来调整原始集合的数值范围到固定的数值范围，然后经过舍入 $\text{round}$ 和截断 $\text{clip}$ 的方式实现取值的离散化，最后重新使用缩放系数 $s$ 来恢复到原始集合的数值范围。使用对称线性量化的好处是：在求解量化问题时需要优化的参数只有量化的缩放系数 $s$，并且量化神经网络在实际进行乘法运算时，可以提取出计算过程中不同的缩放系数 $s$，先进行低精度的整数乘法，然后统一进行缩放运算，这样可以简化运算，实现计算加速效果，如 Figure. 3 所示。
{: width=”90%” loading=”lazy” style=”margin-bottom: 30px;”}
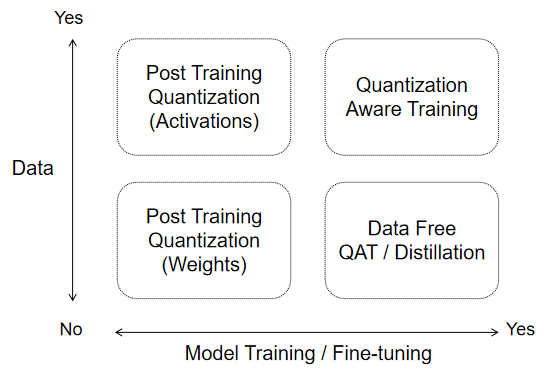
后训练量化和量化感知训练
后训练量化（Post-Training Quantization, PTQ），又称离线量化，指的是将一个预训练的神经网络模型通过参数优化等方法获得一个量化的神经网络模型，一般不会涉及网络的再训练过程。离线量化方法可以快速获取一个量化模型，可以节省训练所需的计算资源，并且更适合快速迭代的应用场景。针对激活值的离线量化需要使用一个小规模的数据集作为校准集（Calibration Dataset），通过对校准集进行推理来统计激活值的数值范围，从而实现对激活的量化优化。
量化感知训练（Quantization-Aware Training，QAT），又称在线量化。与离线量化不同，在线量化将量化映射函数事先插入到模型的计算图中需要被量化的参数的位置，并对模型使用完整的训练集进行训练。再训练过程不仅会优化原始任务的损失，同时也会优化量化误差带来的量化损失。使用量化感知训练得到的量化模型通常比后训练量化得到的模型的预测准确度更高，但需要消耗大量的计算资源，并且超参数的设定也会对量化模型的收敛产生影响。
{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
Hessian 矩阵
海森矩阵（Hessian Matrix），或称作黑塞矩阵、海瑟矩阵等，是由多元函数的二阶偏导数构成的方阵。对于复杂的优化问题，其目标函数往往较为复杂。为了使问题简化，可以将目标函数在某点的邻域进行二阶泰勒展开（Taylor Expansion）来逼近原函数，其中的二阶项就包含 Hessian 矩阵。
例如，对于一个多元函数 $\mathcal{F}(\mathbf{x})$，其在点 $\mathbf{x}_0$ 处的二阶泰勒展开可以表示为：
$$
\begin{align*}
\mathcal{F}(\mathbf{x}) \approx \mathcal{F}(\mathbf{x}_0) + \nabla \mathcal{F}(\mathbf{x}_0)^{T} \cdot \Delta \mathbf{x} + \frac{1}{2} \Delta \mathbf{x}^{T} \cdot \nabla^{2} \mathcal{F}(\mathbf{x}_0) \cdot \Delta \mathbf{x},
\end{align*}
$$
其中的二阶偏导数矩阵 $\mathbf{H}^{(\mathbf{x})} = \nabla^{2} \mathcal{F}(\mathbf{x}_0)$ 就是 $\mathcal{F}$ 在点 $\mathbf{x}_0$ 处的 Hessian 矩阵，$\Delta \mathbf{x} = \mathbf{x} - \mathbf{x}_0$ 是 $\mathbf{x}$ 相对于 $\mathbf{x}_0$ 的偏移量。
在深度神经网络的优化问题中，Hessian 矩阵可以用来描述损失函数在参数空间中的 Loss landscape。已有的工作例如 PyHessian[^1] 通过近似计算 Hessian 矩阵的特征向量（Eigenvalue）、迹（Trace），可以获得关于损失函数的二阶信息，从而更好地对不同模型和优化器的性能进行比较和分析。
本次介绍的三篇论文 AdaRound[^2]、BRECQ[^3]、QDrop[^4] 均使用了 Hessian 矩阵来优化量化神经网络模型的性能。
AdaRound
- Title: Up or Down? Adaptive Rounding for Post Training Quantization
- Venue: ICML 2020
- Author(s): Markus Nagel, Rana Ali Amjad, Mart van Baalen, Christos Louizos, Tijmen Blankevoort
- Institution(s): Qualcomm AI Research
- Link: arxiv:2006.10518
前言
在进行神经网络的后训练量化时，预训练模型的权重参数 $\mathbf{w}$ 和对应的量化缩放系数 $\mathbf{s}$ 已经确定，则对于量化误差 $\Delta \mathbf{w}$ 也已确定。假设预训练模型在原始任务上的全局损失为 $\mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w})$，其中 $\mathbf{x}$ 为输入样本，$\mathbf{y}$ 为预测真值，$\mathbf{w}$ 为模型参数。将对模型参数 $\mathbf{w}$ 的量化看作为对 $\mathbf{w}$ 的一个扰动，即 $Q(\mathbf{w})=\mathbf{w}+\Delta \mathbf{w}$。那么，该预训练模型的量化对全局损失的期望及其二阶泰勒展开的近似可以表示为：
$$
\begin{align*}
& \mathbb{E}[\mathcal{L}(\mathbf{x}, \mathbf{y}, Q(\mathbf{w}))]\\
\overset{(a)}{\approx} & \mathbb{E}[\Delta\mathbf{w}^{T} \cdot \nabla \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w}) + \frac{1}{2} \Delta\mathbf{w}^{T} \cdot \nabla^{2} \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w}) \cdot \Delta\mathbf{w}]\\
= & \Delta \mathbf{w}^{T} \cdot \mathbf{g}^{(\mathbf{w})} + \frac{1}{2} \Delta \mathbf{w}^{T} \cdot \mathbf{H}^{(\mathbf{w})} \cdot \Delta \mathbf{w},
\end{align*}
$$
其中 $\mathbf{g}^{(\mathbf{w})}$ 为原始任务损失 $\mathcal{L}$ 对 $\mathbf{w}$ 的一阶偏导数向量，$\mathbf{H}^{(\mathbf{w})}$ 为 Hessian 矩阵：
$$
\begin{align*}
\mathbf{g}^{(\mathbf{w})} & = \mathbb{E} \left[ \nabla_{\mathbf{w}} \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w}) \right]\\
\mathbf{H}^{(\mathbf{w})} & = \mathbb{E} \left[ \nabla_{\mathbf{w}}^{2} \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w})\right].
\end{align*}
$$
由于使用的是已训练至收敛的预训练模型，可以假设原任务损失对模型参数 $\mathbf{w}$ 的一阶偏导数为 $0$，即泰勒展开一阶项为 $0$。常数项也相互抵消。因此，量化对全局损失的期望可以近似用泰勒展开的二阶项来表示：
$$
\mathbb{E}[\mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w} + \Delta \mathbf{w}) - \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w})] = \frac{1}{2} \Delta \mathbf{w}^{T} \cdot \mathbf{H}^{(\mathbf{w})} \cdot \Delta \mathbf{w}.
$$
这样，针对网络模型参数的量化问题就转化为了对包含 Hessian 矩阵的二次型的优化问题。为了更好地理解这个问题，不妨设 $\mathbf{w}$ 包含两个参数 $\mathbf{w}^{T}=[w_{1}, w_{2}]$，对应的量化误差为 $\Delta \mathbf{w}^{T}=[\Delta w_{1}, \Delta w_{2}]$，若对应的 Hessian 矩阵为：
$$
\mathbf{H}^{(\mathbf{w})} =
\begin{bmatrix}
1 & 0.5 \\
0.5 & 1
\end{bmatrix},
$$
则量化误差对全局损失的影响可以表示为：
$$
\Delta \mathbf{w}^{T} \cdot \mathbf{H}^{(\mathbf{w})} \cdot \Delta \mathbf{w} = \Delta w_{1}^{2} + \Delta w_{2}^{2} + \Delta w_{1} \Delta w_{2},
$$
其中位于 Hessian 矩阵对角线上的二次型项恒为非负，其必然会导致量化误差对全局损失的增加。而 Hessian 矩阵的非对角线项可正可负，会导致量化误差之间的交互作用。若扰动方向相反，则可以使得模型全局损失减小。
{: width=”50%” loading=”lazy” style=”margin-bottom: 30px;”}
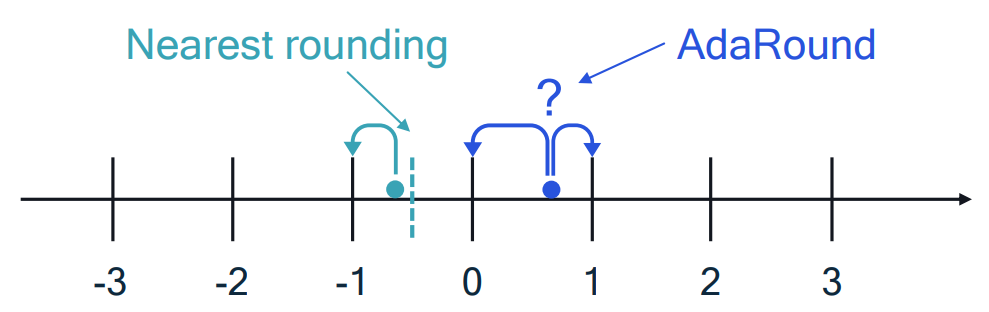
AdaRound 提出了一个全新的模型量化算法的优化视角：传统的就近舍入（Round to Nearest）方法会将量化误差 $\Delta \mathbf{w}$ 的每个分量 $\Delta w_{i}$ 都舍入到最接近的整数值 $Q(\Delta w_{i})$，这并不一定是最优解。如 Figure. 5 所示，通过优化量化误差 $\Delta \mathbf{w}$ 的每个分量的舍入方向（Up or Down），可能会使得量化误差对全局损失的影响更小。
方法
从全局损失到局部损失
AdaRound 将量化误差对全局损失的影响的期望作为优化目标函数：
$$
\begin{align*}
\underset{\Delta \mathbf{w}}{\arg\min} \space \mathbb{E}[\mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w} + \Delta \mathbf{w}) - \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w})]
\end{align*}
$$
该目标函数可以转化为包含 Hessian 矩阵的二次型形式：
$$
\begin{align*}
\underset{\Delta \mathbf{w} ^{(\ell)}}{\arg\min} \space
\mathbb{E}[\Delta {\mathbf{w} ^{(\ell)}} ^{T} \cdot \mathbf{H} ^{(\mathbf{w})} \cdot \Delta \mathbf{w} ^{(\ell)}]
\end{align*}
$$
对于常见粒度的参数量化而言，其 Hessian 矩阵的规模很大，很难在有限时间内进行计算和求解。AdaRound 对该问题进行了简化。首先，AdaRound 将参数粒度限制在了 Layer-wise 层级，即每次优化只考虑一个参数层的所有参数。对于模型的每一层 $\ell$ 中的权重参数 $\mathbf{W}^{(\ell)}$，全局损失 $\mathcal{L}$ 对其的二阶偏导数可以表示为：
$$
\begin{align*}
\frac{\partial^{2} \mathcal{L}}{\partial \mathbf{W} _{i,j} ^{(\ell)} \partial \mathbf{W} _{m,o} ^{(\ell)}} & = \frac{\partial}{\partial \mathbf{W} _{m,o} ^{(\ell)}} \left[ \frac{\partial\mathcal{L}}{\partial \mathbf{z} _{i} ^{(\ell)}} \cdot \mathbf{x} _{j} ^{(\ell-1)} \right] \\
& = \frac{\partial ^{2} \mathcal{L}}{\partial \mathbf{z} _{i} ^{(\ell)} \partial \mathbf{z} _{m} ^{(\ell)}} \cdot \mathbf{x} _{j} ^{(\ell-1)} \cdot \mathbf{x} _{o}^{(\ell-1)},
\end{align*}
$$
那么，损失函数对该层参数的 Hessian 矩阵可以表示为：
$$
\mathbf{H} ^{(\mathbf{W} ^{(\ell)})} = \mathbb{E} \left[ \mathbf{x} ^{(\ell-1)} \cdot {\mathbf{x} ^{(\ell-1)}} ^{T} \otimes \nabla _{\mathbf{z} ^{(\ell)}} ^{2} \mathcal{L} \right],
$$
其中 $\mathbf{x}^{(\ell-1)}$ 为上一层的输出激活值，$\mathbf{z}^{(\ell)}$ 为该层的预激活值，$\otimes$ 表示 Kronecker 积。AdaRound 分别基于两个不同的假设对该 Hessian 矩阵进行了简化。
假设一：Hessian 矩阵 $\mathbf{H} ^{(\mathbf{W} ^{(\ell)})}$ 为对角矩阵，即本层网络的神经元输出相互独立。在此假设下，Hessian 矩阵可以简化为：
$$
\mathbf{H} ^{(\mathbf{W} ^{(\ell)})} = \mathbb{E} \left[\mathbf{x} ^{(\ell-1)}\cdot{\mathbf{x} ^{(\ell-1)}} ^{T}\otimes\text{diag}(\nabla _{\mathbf{z} ^{(\ell)}} ^{2}\mathcal{L} _{i,i}) \right].
$$
假设二：损失函数 $\mathcal{L}$ 对 $\mathbf{z} ^{(\ell)}$ 的二阶偏导数是常数，即与输入激活值 $\mathbf{x} ^{(\ell - 1)}$ 无关。因此 $\nabla _{\mathbf{z} ^{(\ell)}} ^{2} \mathcal{L}$ 是一个常数矩阵。这样目标函数就省略了加权项，最终简化为对当前层预激活输出的均方误差（Mean Squared Error, MSE）的形式：
$$
\begin{align*}
& \underset{\Delta \mathbf{W} _{k,:} ^{(\ell)}}{\arg\min} && \mathbb{E} \left[ \nabla _{\mathbf{z} ^{(\ell)}} ^{2} \mathcal{L} _{k,k} \cdot \Delta \mathbf{W} _{k,:} ^{(\ell)} \mathbf{x} ^{(\ell-1)} {\mathbf{x} ^{(\ell-1)}} ^{T} {\Delta \mathbf{W} _{k,:} ^{(\ell)}} ^{T} \right]\\
=\space & \underset{\Delta \mathbf{W} _{k,:} ^{(\ell)}}{\arg\min} && \Delta \mathbf{W} _{k,:} ^{(\ell)} \mathbb{E} \left[ \mathbf{x} ^{(\ell-1)}{\mathbf{x} ^{(\ell-1)}} ^{T} \right] {\Delta \mathbf{W} _{k,:} ^{(\ell)}} ^{T} \\
=\space & \underset{\Delta \mathbf{W} _{k,:} ^{(\ell)}}{\arg\min} && \mathbb{E} \left[ \left( \Delta \mathbf{W} _{k,:} ^{(\ell)} \mathbf{x} ^{(\ell-1)} \right) ^{2} \right]
\end{align*}
$$
通过以上对问题的简化，原始的全局损失转化为了每一层预激活输出 MSE 的局部损失。这样只需要进行逐层进行优化局部损失，即可完成对量化误差的优化。
AdaRound
为了对舍入方向进行优化，AdaRound 设计了一种对上述局部损失的优化方法。AdaRound 的目标函数为当前层预激活 MSE 加入了一个正则化项。正则化项的参数 $\mathbf{V}$ 是与参数 $\mathbf{W}$ 同维度的可学习参数，用来控制量化误差的舍入方向。AdaRound 的目标函数可以表示为：
$$
\underset{\Delta \mathbf{W}^{(\ell)}}{\arg\min} \space | \mathbf{W}\mathbf{x} - \widetilde{\mathbf{W}}\mathbf{x} | _{F} ^{2} + \lambda f _{reg}(\mathbf{V}),
$$
其中 $\widetilde{\mathbf{W}}$ 是经过量化的权重参数：
$$
\widetilde{\mathbf{W}} = s \cdot \text{clip} \left( \left\lfloor \frac{\mathbf{W}}{s} \right\rfloor + h(\mathbf{V}),n,p \right).
$$
与常规的对称线性量化函数不同，AdaRound 的量化函数将就近舍入改为向下取整后加上一个整流函数 $h$：
$$
h(\mathbf{V} _{i,j}) = \text{clip} \left( \sigma(\mathbf{V} _{i,j})(\zeta - \gamma) + \gamma, 0, 1 \right),
$$
整流函数 $h$ 的输入为 $\mathbf{V}$，输出为普通 Sigmoid 函数 $\sigma$ 经过范围缩放后再进行截断至范围 $[0,1]$ 之间的结果，表示当前参数的自适应舍入方向。这样设计的目的是为了避免 Sigmoid 函数在趋近 $0$ 或 $1$ 时的梯度消失问题。其中，缩放系数 $\zeta$ 和 $\gamma$ 分别设定为 $\zeta=1.1$ 和 $\gamma=-0.1$。
$$
f _{reg} (\mathbf{V}) = \sum _{i,j} 1 - | 2h(\mathbf{V} _{i,j}) - 1 | ^{\beta},
$$
AdaRound 目标函数的正则项 $f _{reg}$ 使用退火温度参数 $\beta$ 来指导可学习参数 $\mathbf{V}$ 的收敛。温度参数 $\beta$ 的值初始化为较大的数值，在初始阶段加大惩罚力度帮助 $\mathbf{V}$ 收敛。之后在优化过程中逐渐减小，进一步优化预激活 MSE。
考虑到神经网络中量化误差会逐层累加，上述优化过程也是逐层进行。为了避免累加的量化误差对最终模型精度的影响，在逐层优化的过程中，当前被量化层的输入是之前所有层经过量化后得到的输出。除此之外，激活函数对量化的影响也需要被考虑到优化范围内。这样就得到了 AdaRound 最终的优化目标函数。
$$
\underset{\mathbf{V}}{\arg\min} \space \left| f _{a}(\mathbf{W} \mathbf{x}) - f _{a}(\widetilde{\mathbf{W}} \hat{\mathbf{x}}) \right| _{F} ^{2} + \lambda f _{reg} (\mathbf{V}),
$$
实验
消融实验
本文从以下五个方面展开了消融实验，验证本文所提出方法的有效性。
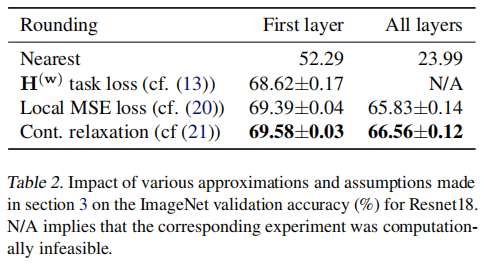
从全局损失到局部损失目标函数的选择。本文对比了原始的就近舍入量化、Hessian 矩阵二次型、预激活 MSE 以及 AdaRound 目标函数的模型参数重建量化效果，结果表明，使用 AdaRound 的目标函数进行优化的量化效果最优。
{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
AdaRound 整流函数 $h$ 的选择。本文对比了使用退火参数的 Sigmoid 函数、普通 Sigmoid 函数加正则项函数以及整流函数 $h$ 加正则化项三种情况，结果表明，使用整流函数 $h$ 加正则化项能够在网络整体的量化上达到更好的效果。
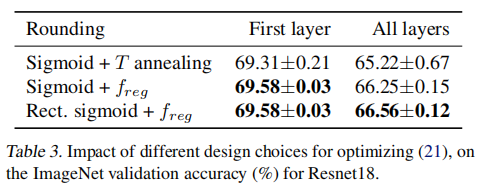{: “width=”40%” loading=”lazy” style=”margin-bottom: 30px;” }
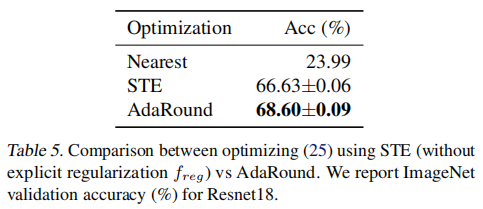
使用 STE 进行优化。本文对比了使用辅助变量进行优化重建的方法以及使用直通估计器（Straight Through Estimator，STE）进行量化感知训练的方法。结果表明，使用重建的方法要比使用 STE 的 QAT 方法效果要更好一些，原因是 STE 可能会导致量化前后的参数反向传播时梯度不匹配（Gradient Mismatch）问题。
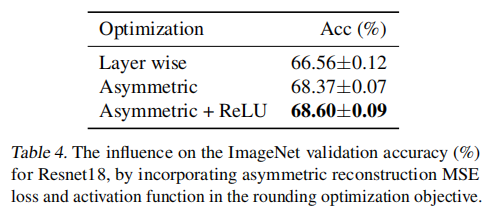{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
优化参数缩放系数的指标。AdaRound 仍然沿用原始的对称线性量化函数，因此在进行重建前需要提前优化确定参数的缩放系数 $s$，一般采用网格搜索的方法来穷举某一目标函数的值，取某种指标的最优值点来确定缩放系数。本文对比了最大最小值差、权重参数 MSE 和激活 MSE 三种指标函数，结果表明，使用权重 MSE 或激活 MSE 对 AdaRound 初始化都能获得较优的量化效果。
{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
校准集样本量大小。本文对校准集的大小对量化的影响进行了探究。结果表明，校准集样本数量越大，量化导致的模型预测损失越低。另外，AdaRound 对校准集的采样来源具有较高的鲁棒性，使用不同任务的数据集作为校准集只会有很微小的精度下降。
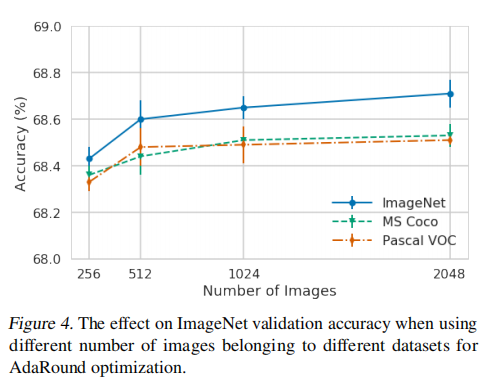{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
对比实验
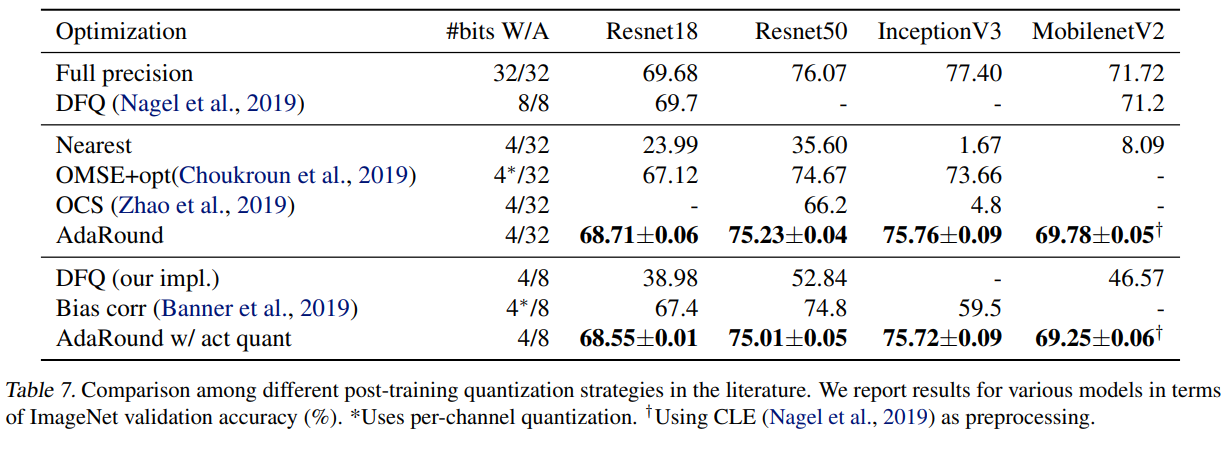
AdaRound 主要对比了 2020 年以前在 ImageNet 图像分类任务上对经典卷积神经网络模型的各种量化方法。结果如下：
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
总结
本文提出了 AdaRound，一种对舍入进行优化的后训练量化方法。同样是对网络的权重参数做优化，不同于过去使用深度学习常用的基于全局损失的梯度下降的优化方式，这种方法采用经过特殊设计的优化目标函数来对一部分可学习参数做微调。这种优化方法也被称为基于重建（Reconstruction）的量化方法。TSQ[^5]、AdaQuant[^6]、Bit Split[^7] 等针对模型量化的研究也使用了类似的基于重建的量化方法。优化相比传统的线性量化方法，AdaRound 在最终量化模型的推理精度上有着明显的提升。
Qualcomm AI 研究院在将 AdaRound 方法用在了其全新推出的深度学习模型部署框架 AIMET[^8] 中作为核心后训练量化算法，推进了深度模型的轻量化发展与实际场景的应用。
BRECQ
- Title: BRECQ: Pushing the Limit of Post-Training Quantization by Block Reconstruction
- Venue: ICLR 2021
- Author(s): Yuhang Li, Ruihao Gong, Xu Tan, Yang Yang, Peng Hu, Qi Zhang, Fengwei Yu, Wei Wang, Shi Gu
- Institution(s): University of Electronic Science and Technology of China, SenseTime Research
- Link: arxiv:2102.05426
前言
AdaRound 为后训练量化算法指明了一个很好的方向：利用包含 Hessian 矩阵的二次型来近似量化的全局损失函数。然而，AdaRound 优化方法仍然存在一些局限性：AdaRound 采用层级的量化粒度，忽略了不同层参数之间的相关性，这样会导致在极低比特量化下模型推理精度大幅下降；另外，AdaRound 在将全局损失转化为局部损失时基于两个强假设，忽略了同一层间不同参数的部分相关性和的相关性，这样实际会损失过多有价值的信息。为了摆脱这些局限性，以获得更好的量化效果，本文在 AdaRound 的基础上提出了新的基于块级重建（Block-wise Reconstruction）的优化方法 BRECQ，对上面提到的问题进行了针对性的改进。
方法
不同层间参数的相关性
神经网络的后训练量化一般选择层级的量化粒度，即网络中的每一个参数化层分别对应一个量化映射，这直观上与深度神经网络层级堆叠的设计结构相吻合，但是却忽略了层级之间的参数的相关性。层级量化本质上是对量化这一全局优化问题的简化，显然，神经网络作为一个优化的整体，层级之间参数的相关性必然会对量化效果产生影响。此时仍可以借助 Hessian 矩阵来探究层级之间参数的相关性。
记神经网络的预激活 $\mathbf{z} ^{(n)} = f(\theta)$，任务损失函数为 $L(f(\theta))$，其中 $\theta$ 为网络的参数。则损失函数对网络中任意参数的二阶偏导数可以表示为：
$$
\frac{\partial^{2} L}{\partial \theta _{i} \partial \theta _{j}} =
\frac{\partial}{\partial \theta _{j}} \left( \sum _{k=1} ^{m} \frac{\partial L}{\partial \mathbf{z} _{k}^ {(n)}} \frac{\partial \mathbf{z} _{k} ^{(n)}}{\partial \theta _{i}} \right) =
\sum _{k=1} ^{m} \frac{\partial L}{\partial \mathbf{z} _{k} ^{(n)}} \frac{\partial ^{2} \mathbf{z} _{k} ^{(n)}}{\partial \theta _{i} \partial \theta _{j}} +
\sum _{k,l=1} ^{m} \frac{\partial \mathbf{z} _{k} ^{(n)}}{\partial \theta _{i}} \frac{\partial ^{2} L}{\partial \mathbf{z} _{k} ^{(n)} \partial \mathbf{z} _{l} ^{(n)}} \frac{\partial \mathbf{z} _{l} ^{(n)}}{\partial \theta _{j}},
$$
由于预训练模型的参数可以看作已经收敛，因此可以假设原任务损失 $L$ 对 $\mathbf{z}$ 的一阶偏导数近似为 $0$，那么，损失函数对任意一组参数的 Hessian 矩阵可以进一步简化为以下的 Guassian-Newton 矩阵形式：
$$
\mathbf{H} ^{(\theta)} \approx \mathbf{G} ^{(\theta)} = \mathbf{J} _{\mathbf{z} ^{(n)}} \left( \theta \right) ^{\text{T}} \mathbf{H} ^{\mathbf{z} ^ {(n)}} \mathbf{J} _{\mathbf{z} ^{(n)}} \left( \theta \right),
$$
其中 $\mathbf{J} _{\mathbf{z} ^{(n)}} (\theta)$ 是预激活 $\mathbf{z}$ 对网络参数 $\theta$ 的 Jacobi 矩阵，$\mathbf{H} ^{\mathbf{z} ^ {(n)}}$ 是预激活 $\mathbf{z}$ 对任务损失 $L$ 的 Hessian 矩阵。这两个矩阵的规模都很大，因此需要对其进行简化。
简化 Jacobi 矩阵 $\mathbf{J}$。考虑量化对网络层输出的扰动 $\Delta \mathbf{z} ^{(n)}$，Jacobi 矩阵 $\mathbf{J}$ 可以看作对 $\Delta \mathbf{z} ^{(n)}$ 进行一阶泰勒展开后的一阶偏导项：
$$
\Delta \mathbf{z} ^{(n)} = \hat{\mathbf{z}} ^{(n)} - \mathbf{z} ^{(n)} \approx \mathbf{J} _{\mathbf{z} ^{(n)}} (\theta) \Delta \theta.
$$
考虑原量化问题的目标函数，即：
$$
\begin{align*}
\underset{\Delta \theta}{\arg\min} \space \Delta \theta ^{\text{T}} \bar{\mathbf{H}} ^{(\theta)} \Delta \theta
\end{align*}
$$
将 Jacobi 矩阵 $\mathbf{J}$ 用泰勒展开的近似式代入，可得简化的量化目标函数：
$$
\begin{align*}
\underset{\hat{\theta}}{\arg\min} \space \Delta \theta ^{\text{T}} \bar{\mathbf{H}} ^{(\theta)} \Delta \theta \approx \underset{\hat{\theta}}{\arg\min} \space \mathbb{E} \left[ \Delta \mathbf{z} ^{(n),\text{T}} \mathbf{H} ^{\mathbf{z} ^ {(n)}} \Delta \mathbf{z} ^{(n)} \right].
\end{align*}
$$
简化 Hessian 矩阵 $\mathbf{H}$。本文提出使用 Fisher 信息矩阵（Fisher Information Matrix，FIM）来近似预激活 $\mathbf{z}$ 对网络参数 $\theta$ 的 Hessian 矩阵。
给定一个概率模型 $p(x|\theta)$，使用已知的观测样本通过极大似然估计（Maximum Likelyhood Estimate）对参数 $θ$ 进行优化，使得观测样本出现概率取极大值。相当于使评分函数 $s(θ)$，即对数似然函数对参数 $θ$ 的一阶偏导数趋近 $0$。Fisher 信息定义为该一阶偏导数的二阶矩，在一般情况下，对数似然函数对参数 $θ$ 的一阶偏导数的期望为 $0$，因此 Fisher 信息也可以表示为概率模型对参数极大似然估计的评分函数 $s$ 的方差。对于所有参数 $θ$，FIM 表示如下：
$$
\bar{\mathbf{F}} ^{(\theta)} = \mathbb{E} \left[ \nabla _{\theta} \log p _{\theta} (y|x) \nabla _{\theta} \log p _{\theta} (y|x) ^{\text{T}} \right] = - \mathbb{E} \left[ \nabla _{\theta} ^{2} \log p _{\theta} (y|x) \right] = -\bar{\mathbf{H}} _{\log p(x|\theta)} ^{(\theta)}.
$$
可以看出，FIM 也可以等价于概率模型的对数似然函数的 Hessian 矩阵的期望的负值。因此，在二阶优化方法中，FIM 一般可以作为 Hessian 矩阵的近似替代。深度神经网络模型的优化方法与概率模型的极大似然估计方法类似，如果能够尽量保证训练样本的分布尽量接近真实数据分布，并且预训练模型参数已经在训练集上收敛，那么就可以使用 FIM 来近似 Hessian 矩阵 $\mathbf{H}$。
Adam 优化器使用了参数梯度的二阶矩估计来为不同的参数设计独立的自适应学习率，在计算中使用梯度的平方，即 FIM 的对角元素。本文采用类似的思想，使用了 FIM 的对角元素组成的对角矩阵来替换 Hessian 矩阵。一个直观的解释是，梯度平方的值越大，该参数参与量化重建的重要性越高。替换后的优化目标函数变为：
$$
\underset{\hat{\mathbf{w}}}{\min} \space \mathbb{E} \left[ \Delta \mathbf{z} ^{(\ell), \text{T}} \mathbf{H} ^{(\mathbf{z} ^{(\ell)})} \Delta \mathbf{z} ^{(\ell)} \right] =
\underset{\hat{\mathbf{w}}}{\min} \space \mathbb{E} \left[ \Delta \mathbf{z} ^{(\ell), \text{T}} \text{diag}(\mathbf{F} ^{(\mathbf{w})}) \Delta \mathbf{z} ^{(\ell)} \right].
$$
块级重建
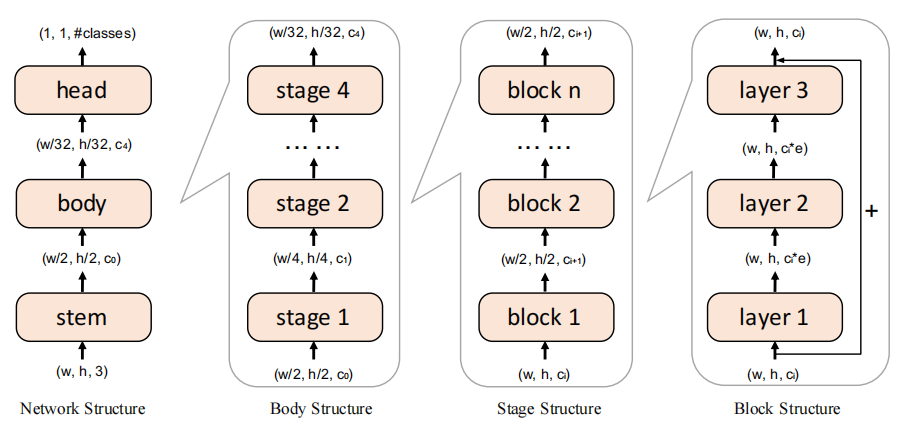
前面提到，基于层级的量化重建会损失不同层参数之间的相关性信息，因此需要探究合适的量化粒度来权衡量化优化问题的规模与层级间相关性损失。本文分析了四种不同的量化重建粒度，从大到小依次为整网（Network-wise）重建、阶段（Stage-wise）重建、块级（Block-wise）重建和层级（Layer-wise）重建，不同粒度的规模如 Figure. 7 所示。
{: width=”60%” loading=”lazy” style=”margin-bottom: 30px;”}
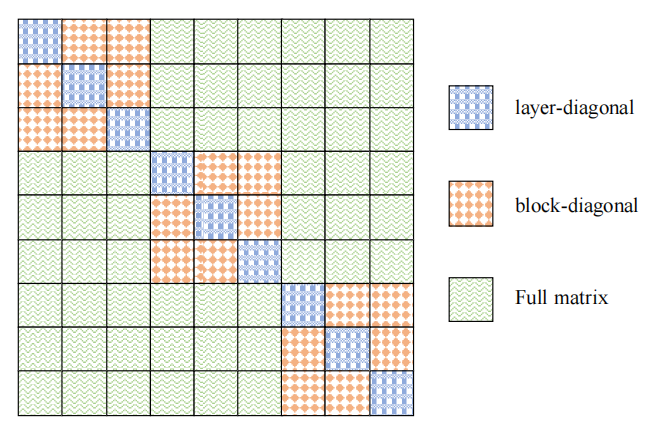
不同的重建粒度，其 Hessian 矩阵的规模也不同。如 Figure. 8 所示，块级或层级的 Hessian 矩阵相当于整网参数的 Hessian 矩阵的分块对角矩阵。
{: width=”50%” loading=”lazy” style=”margin-bottom: 30px;”}
本文对上述四种不同量化粒度的参数重建进行了实验，发现使用块级重建粒度的量化效果最优。使用块级重建的优越性可以从两方面解释。第一，ResNet 等网络采用的残差连接（Residual Connection）可能会加强块级参数的相关性；第二，校准集一般规模较小，要比起粒度更大的阶段或整网重建，块级粒度的参数重建更不容易发生过拟合现象。本文将这种基于块级重建的量化方法称为 BRECQ。
实验
消融实验
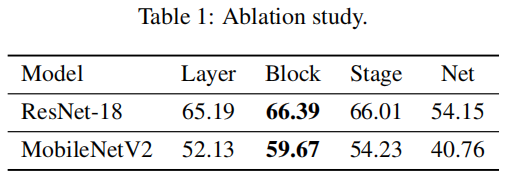
本文对上面提到的四种不同的重建粒度进行了消融实验。在 ImageNet 图像分类任务上对 ResNet-18 和 MobileNet-V2 模型进行 2-bit 量化，结果见 Table. 2。结果表明，块级重建的量化效果要比其它粒度的效果要好。
{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
对比实验
本文在 ImageNet 图像分类任务和 MS COCO 目标检测任务上展开工作。
在 ImageNet 图像分类任务上的对比结果如下：
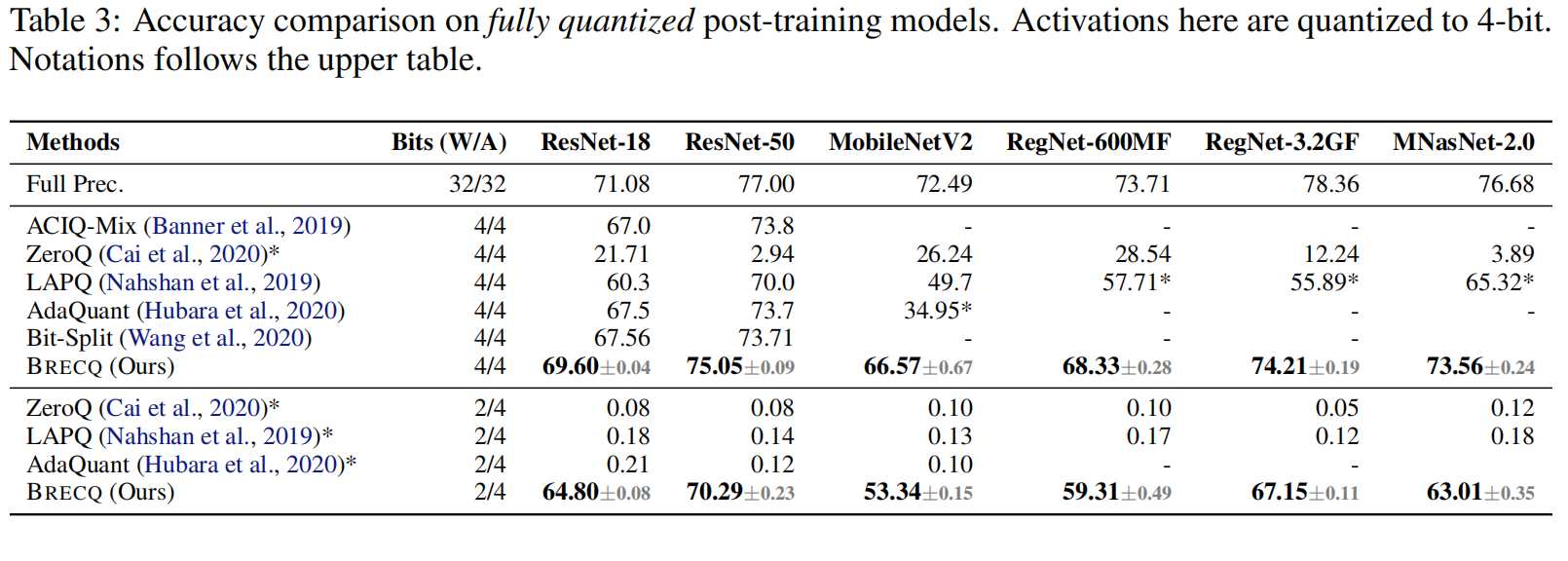{: width=”90%” loading=”lazy” style=”margin-bottom: 30px;”}
在 MS COCO 目标检测任务上的对比结果如下：
{: width=”90%” loading=”lazy” style=”margin-bottom: 30px;”}
总结
本文提出了 BRECQ，一种由 AdaRound 改进而来的基于块级重建的后训练量化方法。BRECQ 设计了新的优化目标函数，充分考虑了块内参数之间的相关性，弥补了层级重建中层级间的参数相关性的损失。BRECQ 的量化效果要显著优于比 AdaRound 以及其它的基于重建的量化方法。
商汤科技模型部署与工具链团队在将 BRECQ 方法作为后训练量化算法的示例整合到了他们推出的开源模型量化框架 MQBench[^9] 中。
QDrop
- Title: QDrop: Randomly Dropping Quantization for Extremely Low-bit Post-Training Quantization
- Venue: ICLR 2022
- Author(s): Xiuying Wei, Ruihao Gong, Yuhang Li, Xianglong Liu, Fengwei Yu
- Institution(s): State Key Lab of Software Development Environment, Beihang University, SenseTime Research
- Link: arxiv:2203.05740
前言
常规的 PTQ 方法对网络权重和激活的量化是相互独立的，一般的流程是先量化权重值，再量化激活值。AdaRound 和 BRECQ 方法与传统 PTQ 方法类似，它们都是先对网络权重参数进行重建，然后使用传统方法对激活值进行量化。这种 PTQ 流程忽略了激活量化对权重量化的影响，依然存在改进空间。本文提出的 QDrop 在 BRECQ 的基础上进行了改进，将对网络权重的重建和对激活量化的优化结合在一起，充分考虑到了整体的量化损失。QDrop 的量化效果在量化不友好的网络（例如 MobileNet-V2）上显著超越了之前的方法。
方法
激活量化如何影响权重量化
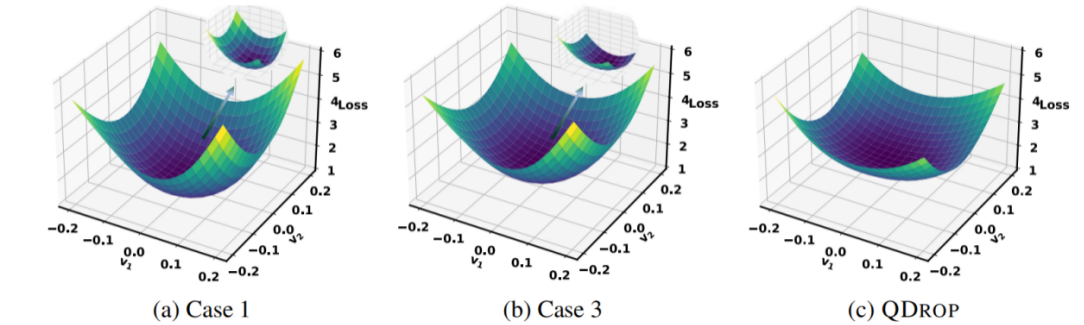
为了验证激活量化对权重参数重建的影响，本文首先基于 BRECQ 方法针对三种不同的激活量化策略开展了对比实验进行观察，三种激活量化策略如下，示意图和结果如 Figure. 9 所示。
- Case 1：原始的 BRECQ 方法。重建时不对激活进行量化；
- Case 2：对当前重建的块以及之前的所有重建完毕的块的激活进行量化。
- Case 3：对当前重建的块之前的所有重建完毕的块的激活进行量化，不对当前块的激活进行量化。
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;” }
实验表明，Case 3 的量化效果最好。也就是说，如果在参数重建的过程中对部分块进行激活量化，有可能提高量化效果。
类似于之前对权重量化的数学定义，对激活的量化也可以定义为对其的扰动，记为 $e=(\hat{a} - a)$，
本文将该扰动由减法形式转化为乘法形式，即 $\hat{a} = a \cdot (1+u)$。定义同时对权重和激活的量化扰动的全局损失为 $L(\boldsymbol{w} + \Delta \boldsymbol{w}, \boldsymbol{x}, \mathbf{1} + \boldsymbol{u}(\boldsymbol{x}))$，那么量化要优化的目标函数为：
$$
\min _{\hat{\boldsymbol{w}}} \mathbb{E} _{\boldsymbol{x}\sim\mathcal{D} _{c}} [L(\boldsymbol{w} + \Delta \boldsymbol{w}, \boldsymbol{x}, \boldsymbol{1} + \boldsymbol{u}(\boldsymbol{x})) - L(\boldsymbol{w}, \boldsymbol{x}, \boldsymbol{1})].
$$
卷积、全连接等线性变换层的运算均可以用矩阵乘法 $\boldsymbol{y}=\boldsymbol{W}\boldsymbol{a}$ 来表示。对激活 $\boldsymbol{a}$ 加入的扰动 $\boldsymbol{u}(\boldsymbol{x})$ ，可以传递到对权重 $\boldsymbol{W}$ 上：
$$
\boldsymbol{W}(\boldsymbol{a} \odot
\begin{bmatrix}
1 + \boldsymbol{u} _{1}(\boldsymbol{x}) \\
1 + \boldsymbol{u} _{2}(\boldsymbol{x}) \\
… \\
1 + \boldsymbol{u} _{n}(\boldsymbol{x})
\end{bmatrix})
= (\boldsymbol{W} \odot
\begin{bmatrix}
1 + \boldsymbol{u} _{1}(\boldsymbol{x}) & 1 + \boldsymbol{u} _{2} (\boldsymbol{x}) & … & 1 + \boldsymbol{u} _{n}(\boldsymbol{x}) \\
1 + \boldsymbol{u} _{1}(\boldsymbol{x}) & 1 + \boldsymbol{u} _{2} (\boldsymbol{x}) & … & 1 + \boldsymbol{u} _{n}(\boldsymbol{x}) \\
… \\
1 + \boldsymbol{u} _{1}(\boldsymbol{x}) & 1 + \boldsymbol{u} _{2} (\boldsymbol{x}) & … & 1 + \boldsymbol{u} _{n}(\boldsymbol{x})
\end{bmatrix})
\boldsymbol{a}.
$$
目标函数可以进一步转化为：
$$
\mathbb{E} _{\boldsymbol{x}\sim\mathcal{D} _{c}} [L (\hat{\boldsymbol{w}}, \boldsymbol{x}, \mathbf{1} + \boldsymbol{u}(\boldsymbol{x})) - L(\boldsymbol{w}, \boldsymbol{x}, \boldsymbol{1})] \approx \mathbb{E} _{\boldsymbol{x}\sim\mathcal{D} _{c}} [L(\hat{\boldsymbol{w}} \odot(\mathbf{1} + \boldsymbol{v}(\boldsymbol{x})), \boldsymbol{x}, \boldsymbol{1}) - L(\boldsymbol{w}, \boldsymbol{x}, \boldsymbol{1})],
$$
$$
\begin{align*}
\mathbb{E} _{\boldsymbol{x} \sim \mathcal{D} _{c}} [L(\hat{\boldsymbol{w}}, \boldsymbol{x}, \boldsymbol{1} + \boldsymbol{u}(\boldsymbol{x})) - L(\boldsymbol{w}, \boldsymbol{x}, \boldsymbol{1})] &\approx \\
\mathbb{E} _{\boldsymbol{x} \sim \mathcal{D} _{c}} [\underbrace{(L(\hat{\boldsymbol{w}}, \boldsymbol{x}, \boldsymbol{1}) - L(\boldsymbol{w},\boldsymbol{x}, \boldsymbol{1}))} _{(7-1)} &+ \underbrace{(L(\hat{\boldsymbol{w}} \odot (\boldsymbol{1} + \boldsymbol{v}(\boldsymbol{x})), \boldsymbol{x}, \boldsymbol{1}) - L(\hat{\boldsymbol{w}}, \boldsymbol{x}, \boldsymbol{1}))} _{(7-2)}]
\end{align*}
$$
上式的第一项为权重参数重建的损失，第二项为参数重建后的网络再加入激活量化之后的损失。也就是说，通过乘法项引入的对激活的量化扰动，对整体的量化损失是有影响的。
可以从量化扰动鲁棒性的角度来理解由激活引入的第二项损失。对激活的量化可以看作对参数重建后的量化网络加入的噪声。如果在输入加入了噪声的情况下进行优化，网络参数优化时的损失平面理论上会更加平坦，即鲁棒性更强。这也解释了前面对比实验中 Case 2 和 Case 3 比第一种情况的效果更好的原因。
QDrop
本文提出了一种权重和激活量化相结合的参数重建优化方案，命名为 QDrop。QDrop 是从前文所述的对比实验的第三种情况加以改进得到的。与原先不同的是，QDrop 对当前重建的层也加入了对输入激活的量化，但是只会以一定的概率 $p$ 来决定输入的每一个元素是否不进行量化，类似于深度学习中的 Dropout，即：
$$
\mathrm{QDROP}:u=
\begin{cases}
0 & \text{with probability }p \\
\frac{\hat{a}}{a}-1 & \text{with probability }1-p &
\end{cases}.
$$
使用 QDrop 得到的参数优化损失平面与其它情况的对比如 Figure. 10 所示。可以看到，使用 QDrop 方法的损失平面要比之前更加平坦。
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
实验
消融实验
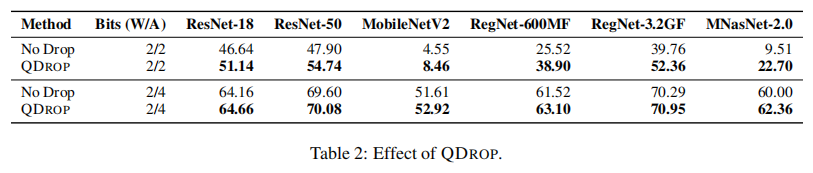
QDrop 与 No Drop。本文对比了使用 QDrop 方法进行随机地激活量化和完全进行激活量化的效果。结果如表所示。结果表明使用 QDrop 后预测精度有所提升。
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
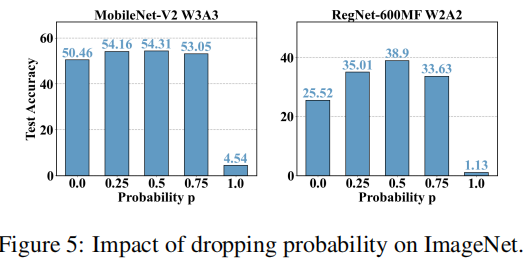
QDrop 概率 $p$ 的选择。本文对 QDrop 概率 $p$ 的选择进行了消融实验，结果如图所示。结果表明，QDrop 概率 $p$ 的值对量化效果有较大影响，过小或过大的概率都会导致量化效果下降。
可以看出，当 $p=0.5$ 时量化模型的预测精度最高。但对于更细粒度的搜索空间本文未作过多讨论。
{: width=”40%” loading=”lazy” style=”margin-bottom: 30px;”}
对比实验
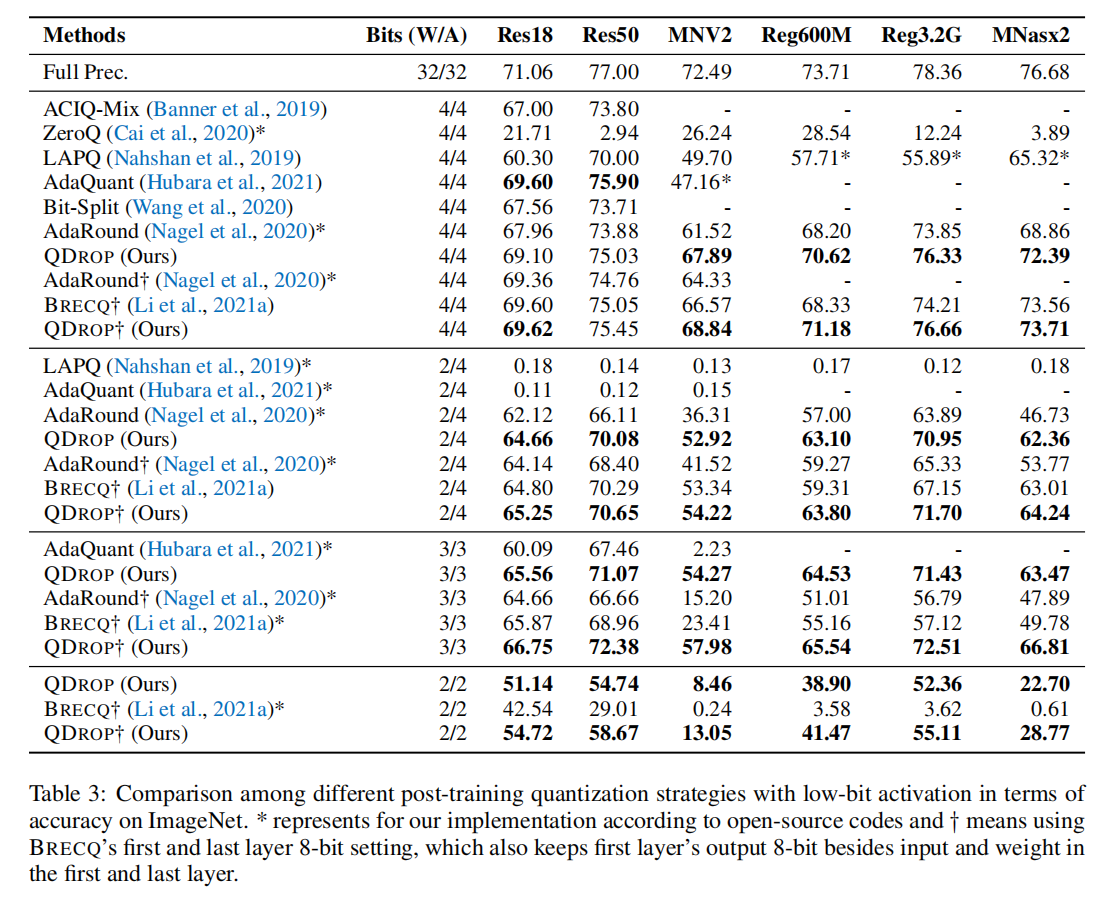
QDrop 在 ImageNet 图像分类任务、MS COCO 目标检测任务和各个自然语言处理任务上展开工作。
在 ImageNet 图像分类任务上的对比结果如下：
{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
在 MS COCO 目标检测任务上的对比结果如下：
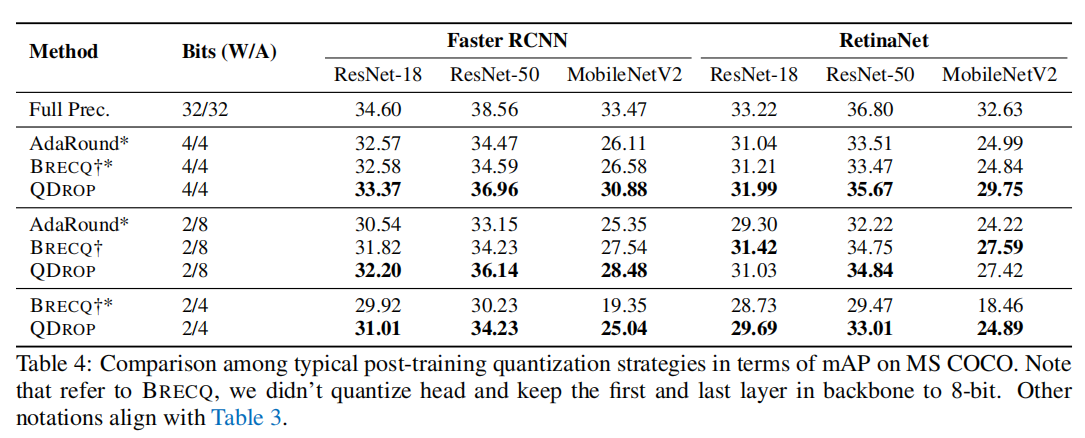{: width=”80%” loading=”lazy” style=”margin-bottom: 30px;”}
在各个自然语言处理任务上的对比结果如下：
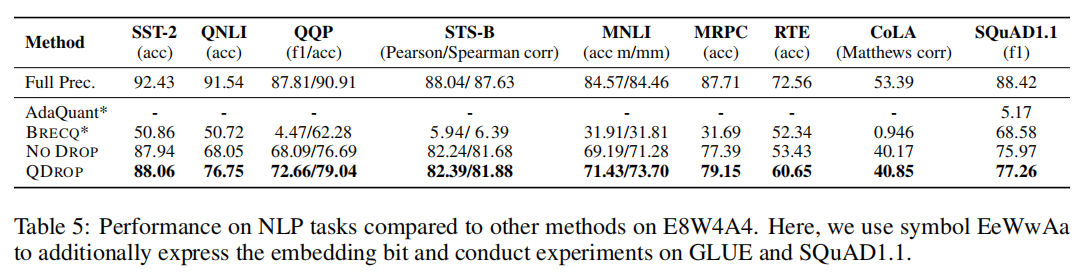{: width=”90%” loading=”lazy” style=”margin-bottom: 30px;”}
总结
本文提出了 QDrop，一种由 BRECQ 改进而来的基于块级重建的后训练量化方法。基于重建的优化方法相比过去的 PTQ 方法的一个优势在于，激活量化和权重量化可以同时进行。QDrop 将对激活的量化与对权重的重建结合到了一起，充分考虑了量化任务对网络模型的整体影响，最终的量化效果达到了 PTQ 方法的新极限。
商汤科技模型部署与工具链团队在 ICLR 2022 发表相关研究论文之后，将 QDrop 方法作为后训练量化算法的示例整合到了他们推出的开源模型量化框架 MQBench 中，并将在之后陆续支持对 NLP 相关任务的网络模型的量化。
参考文献
[^1]: Zhewei Yao, Amir Gholami, Kurt Keutzer, et al. PyHessian: Neural Networks Through the Lens of the Hessian. BigData 2020.
[^2]: Markus Nagel, Rana Ali Amjad, Mart van Baalen, et al. Up or Down? Adaptive Rounding for Post-Training Quantization. ICML, 2020.
[^3]: Yuhang Li, Ruihao Gong, Xu Tan, et al. BRECQ: Pushing the Limit of Post-Training Quantization by Block Reconstruction. ICLR, 2021.
[^4]: Xiuying Wei, Ruihao Gong, Yuhang Li, et al. QDrop: Randomly Dropping Quantization for Extremely Low-bit Post-Training Quantization. ICLR, 2022.
[^5]: Peisong Wang, Qinghao Hu, Yifan Zhang, et al. Two-Step Quantization for Low-bit Neural Networks. CVPR 2018.
[^6]: Itay Hubara, Yury Nahshan, Yair Hanani, et al. Improving Post Training Neural Quantization: Layer-wise Calibration and Integer Programming. ICML, 2021.
[^7]: Peisong Wang, Qiang Chen, Xiangyu He, et al. Towards Accurate Post-training Network Quantization via Bit-Splitting and Stitching. ICML, 2020.
[^8]: Sangeetha Siddegowda, Marios Fournarakis, Markus Nagel, et al. Neural Network Quantization with AI Model Efficiency Toolkit (AIMET). ArXiv, 2022, abs/2201.08442.
[^9]: Yuhang Li, Mingzhu Shen, Yan Ren, et al. MQBench: Towards Reproducible and Deployable Model Quantization Benchmark. NeurIPS Track on Datasets and Benchmarks, 2021.